Hai điện tích \[{q_1} = {6.10^{ - 8}}C;{q_2} = {2.10^{ - 8}}C\] đặt tại 2 điểm A và B cách nhau 30 cm trong chân không. Tính cường độ điện trường tổng hợp do điện tích q1và q2gây ra tại M với M nằm trên AB và AM = 60 cm; BM = 30 cm.
![Hai điện tích \[{q_1} = {6.10^{ - 8}}C;{q_2} = {2.10^{ - 8}}C\] đặt tại 2 điểm A và B cách nhau 30 cm trong chân không. Tính cường độ điện trường tổng hợp do điện tích q1và q2gây ra tại M vớ (ảnh 1)](https://video.vietjack.com/upload2/images/1647819580/1647819748-image1.png)
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Lời giải
Tóm tắt:
q1= 6.10-8 C; q2= 2.10-8 C
AB = 30 cm = 0,3 m
AM = 60 cm = 0,6 m
BM = 30 cm = 0,3 m
Hỏi: EM= ?
Lời giải:
![Hai điện tích \[{q_1} = {6.10^{ - 8}}C;{q_2} = {2.10^{ - 8}}C\] đặt tại 2 điểm A và B cách nhau 30 cm trong chân không. Tính cường độ điện trường tổng hợp do điện tích q1và q2gây ra tại M vớ (ảnh 2)](https://video.vietjack.com/upload2/images/1647819580/1647819748-image2.png) Ta có: AM = AB + BM
Ta có: AM = AB + BM
Gọi \(\overrightarrow {{E_{AM}}} ,\overrightarrow {{E_{BM}}} \) là cường độ điện trường do điện tích điểm q1, q2đặt tại A, B gây ra tại M (\(\overrightarrow {{E_{AM}}} ,\overrightarrow {{E_{BM}}} \)có phương chiều như hình vẽ)
Theo nguyên lý chồng chất điện trường, cường độ điện trường tổng hợp tại M là:\[\overrightarrow {{E_M}} = \overrightarrow {{E_{AM}}} + \overrightarrow {{E_{BM}}} \]
Vì \[\overrightarrow {{E_{AM}}} \],\[\overrightarrow {{E_{BM}}} \]cùng phương, cùng chiều nên: \({E_M} = {E_{AM}} + {E_{BM}}\)
Với \({E_{AM}} = \frac{{\left| {k{q_1}} \right|}}{{\varepsilon .A{M^2}}} = \frac{{\left| {{{9.10}^9}{{.6.10}^{ - 8}}} \right|}}{{1.{{\left( {0,6} \right)}^2}}} = 1500\left( {V/m} \right)\)
\({E_{BM}} = \frac{{\left| {k{q_2}} \right|}}{{\varepsilon .B{M^2}}} = \frac{{\left| {{{9.10}^9}{{.2.10}^{ - 8}}} \right|}}{{1.{{\left( {0,3} \right)}^2}}} = 2000\left( {V/m} \right)\)
Vậy cường độ điện trường tổng hợp tại M là: \({E_M} = 1500 + 2000 = 3500\left( {V/m} \right)\)
Cho đoạn mạch như hình vẽ:
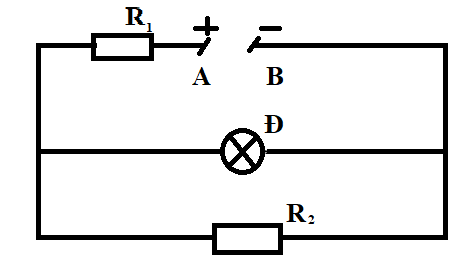
R1= 4Ω , R2= 9Ω , Đèn ghi 6 V- 12 W (bỏ qua điện trở dây nối).
Đặt vào hai đầu đoạn mạch AB một hiệu điện thế không đổi 18 V.