Từ các số 5, 0, 1, 3, viết các số tự nhiên có ba chữ số khác nhau thỏa mãn điều kiện:
a) Các số đó chia hết cho 5;
b) Các số đó chia hết cho 3.
Giải bởi qa.haylamdo.com
a) Gọi số tự nhiên cần tìm có ba chữ số khác nhau là
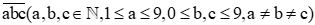
Vì số đó chia hết cho 5 nên chữ số tận cùng là 0 hoặc 5. Do đó c = 0 hoặc c = 5.
+) Với c = 0, ta có bảng chữ số a, b khác nhau và khác 0 thỏa mãn là:
a | 1 | 5 | 3 | 5 | 1 | 3 |
b | 5 | 1 | 5 | 3 | 3 | 1 |
Do đó ta thu được các số: 150; 510; 350; 530; 130; 310.
+) Với c = 5, a 0 nên a = 1 hoặc 3, ta có bảng chữ số a, b khác nhau thỏa mãn là:
a | 1 | 3 | 1 | 3 |
b | 0 | 0 | 3 | 1 |
Do đó ta thu được các số: 105; 305; 135; 315
Vậy các số tự nhiên có ba chữ số khac nhau chia hết cho 5 được viết từ các chữ số đã cho: 130; 135; 105; 150; 310; 315; 350; 305; 510; 530.
b) Gọi số tự nhiên cần tìm có ba chữ số khác nhau là
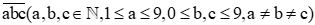
Vì số đó chia hết cho 3 nên tổng các chữ số của nó phải chia hết cho 3 hay (a + b + c) chia hết cho 3.
Ta thấy cặp 3 chữ số khác nhau có tổng chia hết cho 3 là: (5, 0, 1); (5, 1, 3) vì (5 + 0 + 1 = 6 chia hết cho 3 và 5 + 1 + 3 = 9 chia hết cho 3)
+) Với (5, 0, 1) ta có các số cần tìm là: 105; 150; 510; 501
+) Với (5, 1, 3) ta có các số cần tìm là: 135; 153; 351; 315; 513; 531
Vậy các số tự nhiên có ba chữ số khac nhau chia hết cho 3 được viết từ các chữ số đã cho: 135; 153; 351; 315; 513; 531; 105; 150; 510; 501.
Trong các số sau: 16; 17; 20; 21; 23; 97. Có bao nhiêu số là hợp số?
Hoàn thành phát biểu sau: “Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có …”:
Phân tích 70 ra thừa số nguyên tố ta được: 70 = . Tổng x + y + z = ?
Một lớp có 30 học sinh. Cô giáo muốn chia lớp thành các nhóm để thực hiện các dự án học tập nhỏ. Biết rằng, các nhóm đều có số người bằng nhau, số người trong một nhóm là các số nguyên tố. Hỏi có bao nhiêu cách chia?
Bạn Nam phân tích số 120 ra thừa số nguyên tố như sau: 120 = .3.5.
Bạn An phân tích 105 ra thừa số nguyên tố như sau: 105 = 3.5.7.
Chọn đáp án đúng.
Có bao nhiêu khẳng định đúng trong các khẳng định sau?
a) Ước nguyên tố của 18 là 1; 2; và 3.
b) Tích của hai số nguyên tố bất kì luôn là số lẻ.
c) Mọi số chẵn đều là hợp số.
Một lớp có 30 học sinh. Cô giáo muốn chia lớp thành các nhóm để thực hiện các dự án học tập nhỏ. Biết rằng, các nhóm đều có số người bằng nhau và có nhiều hơn 1 người trong mỗi nhóm. Hỏi mỗi nhóm có thể có bao nhiêu người?
Trong các số đã cho dưới đây, số nào là số nguyên tố, số nào là hợp số? Vì sao?
190; 11; 132; 23; 43; 17; 21.
