Quan sát Hình 4.3a.
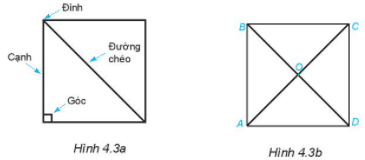
1. Nêu tên các đỉnh, cạnh, đường chéo của hình vuông ABCD (H.4.3b)
2. Dùng thước thẳng đo và so sánh độ dài các cạnh của hình vuông; hai đường chéo của hình vuông.
3. Dùng thước đo góc để đo và so sánh các góc của hình vuông.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
1. Hình vuông ABCD có
Các đỉnh: A, B, C, D
Các cạnh: AB, BC, CD, DA
Các đường chéo: AC, BD
2. Sau khi dùng thước thẳng đo ta nhận thấy:
+) AB = BC = CD = AD nghĩa là độ dài các cạnh của hình vuông đều bằng nhau.
+) AC = BD, nghĩa là độ dài 2 đường chéo của hình vuông bằng nhau.
3. Sau khi sử dụng thước đo góc là ê ke để đo ta nhận thấy: các góc A, góc B, góc C, góc D đều bằng 90o nghĩa là các góc của hình vuông đều bằng nhau và bằng .
Trong các hình vẽ dưới đây, Có bao nhiêu hình là hình lục giác đều?

Cho phát biểu sau: “……….. là hình có ba cạnh bằng nhau và ba góc bằng nhau bằng . Điền từ thích hợp vào chỗ trống.
Hình lục giác đều có đường chéo chính dài 18 cm. Số đo cạnh của hình lục giác đều là:
Nối cột A với cột B để được các bước vẽ hình vuông 7cm một cách chính xác:
Cột A |
| Cột B |
1) Bước 1 | a) Vẽ đường thẳng đi qua B vuông góc với AB. Trên đường thẳng này lấy điểm C sao cho BC bằng 7cm. | |
2) Bước 2 | b) Nối điểm B với điểm C lại ta được hình vuông ABCD cạnh 7cm. | |
3) Bước 3 | c) Vẽ cạnh AB bằng 7cm | |
4) Bước 4 | d) Vẽ đường thẳng đi qua A vuông góc với AB. Trên đường thẳng này lấy điểm D sao cho AD bằng 7cm |
Sắp xếp các bước vẽ hình tam giác đều cạnh 2cm:
1) Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 2cm.
2) Vẽ đoạn thẳng AB bằng 2cm.
3) Nối các điểm A với C, B với C ta được tam giác đều ABC cạnh 2 cm.
4) Hai đường tròn tâm A và tâm B cắt nhau tại điểm C.
Có bao nhiêu tính chất dưới đây là của hình vuông?
i) Hình vuông có bốn cạnh bằng nhau.
ii) Hình vuông có bốn góc bằng nhau và bằng .
iii) Hình vuông có hai đường chéo bằng nhau.
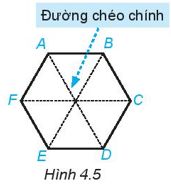
Hãy quan sát Hình 4.5.
1. Hãy kể tên các đường chéo chính của hình lục giác đều ABCDEF.
2. Hãy so sánh độ dài các đường chéo chính với nhau.
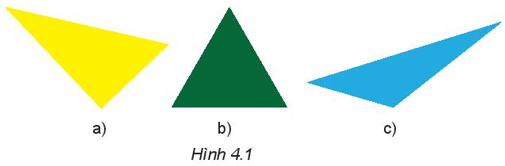
Trong các hình dưới đây (H.4.1), hình nào là tam giác đều?
Em hãy tìm một số hình ảnh hình tam giác đều trong thực tế.