Quan sát hình bình hành ở Hình 4.12a.
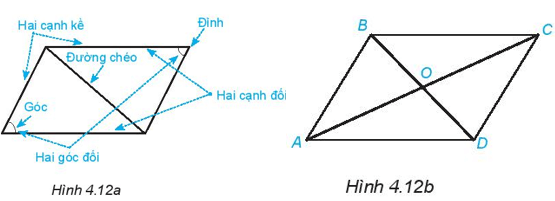
1. Đo và so sánh độ dài các cạnh đối của hình bình hành ABCD (H.4.12b)
2. Đo và so sánh OA với OC, OB với OD.
3. Các cạnh đối của hình hình hành ABCD có song song với nhau không?
4. Các góc đối của hình bình hành ABCD có bằng nhau không?
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
1. Sau khi sử dụng thước thẳng để đo đoạn thẳng, ta nhận thấy: AB = CD; BC = AD, nghĩa là các cạnh đối của hình bình hành bằng nhau.
2. Sau khi sử dụng thước thẳng để đo đoạn thẳng, ta nhận thấy: OA = OC; OB = OD
3.
+) Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+) Khi đặt eke vuông góc với BC ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Nghĩa là các cạnh đối của hình bình hành song song với nhau.
4. Bằng cách gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.
Có bao nhiêu tính chất dưới đây là tính chất của hình thang cân?
a) Trong hình thang cân có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
b) Trong hình thang cân có hai đường chéo bằng nhau.
c) Trong hình thang cân có hai góc kề một đáy bằng nhau.
d) Trong hình thang cân có hai cặp cạnh đối song song với nhau.
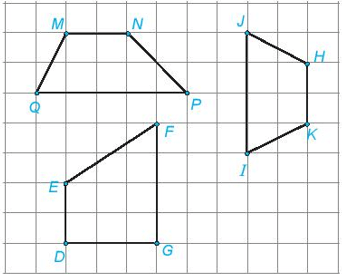
Hình nào trong các hình đã cho là hình thang cân? Hãy cho biết tên hình thang cân đó
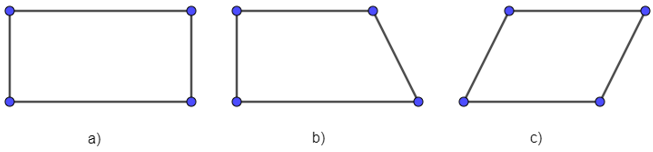
Quan sát hình sau và cho biết hình nào là hình chữ nhật, hình nào là hình thoi?
Các bước vẽ hình bình hành DEFG có DE = 4cm; EF = 3cm như sau:
Bước 1. Vẽ đoạn DE = 3cm.
Bước 2. Vẽ đường thẳng đi qua E. Trên đường thẳng này lấy điểm F sao cho EF = 3cm.
Bước 3. Vẽ đường thẳng đi qua D và song song với EF. Trên đường thẳng này lấy điểm G sao cho DG = EF = 3cm.
Bước 4. Nối điểm G với điểm F lại ta được hình bình hành DEFG.
Trong các bước vẽ trên có bao nhiêu bước làm đúng?
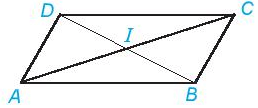
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại điểm I. Sử dụng compa hoặc thước thẳng kiểm tra xem điểm I có là trung điểm của hai đường chéo AC và BD không?