Cùng một lúc ở hai điểm cách nhau 300 m, có hai ô tô đi ngược chiều nhau. Xe thứ nhất đi từ A có tốc độ ban đầu là 10 m/s, xe thứ hai đi từ B với tốc độ ban đầu là 20 m/s. Biết xe đi từ A chuyển động nhanh dần đều, xe đi từ B chuyển động chậm dần đều và hai xe chuyển động với gia tốc có cùng độ lớn 2 m/
a) Viết phương trình chuyển động của mỗi xe.
b) Tính khoảng cách giữa hai xe sau 5s.
c) Hai xe gặp nhau sau thời gian bao lâu kể từ lúc xuất phát. Khi đó vị trí hai xe gặp nhau cách vị trí ban đầu của xe thứ nhất một khoảng bằng bai nhiêu ?
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
a) Chọn Ox có gốc tại A, chiều dương hướng từ A sang B. Gốc thời gian là lúc hai xe bắt đầu chuyển động. Suy ra = 0; = 300 m.
- Với xe thứ nhất chuyển động theo chiều dương của Ox nên: = 10m/s và chuyển động nhanh dần đều nên = 2 m/ (do > 0) (0,25đ)
- Xe thứ hai chuyển động theo chiều âm của Ox nên = - 20 m/s và chuyển động chậm dần đều nên = 2 m/ (do < 0), = 300 m. (0,25đ)
Phương trình chuyển động của xe thứ nhất:
Phương trình chuyển động của xe thứ hai:
b) Khoảng cách giữa hai xe:
c) Hai xe gặp nhau khi: 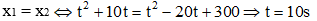
Vậy hai xe gặp nhau sau 10s.
Khi đó thay t = 10s vào ta có: 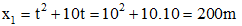
Suy ra vị trí gặp nhau cách vị trí xuất phát ban đầu của xe thứ 1 là 200 m.
Một vật đang nằm trên mặt phẳng nằm ngang, dưới tác dụng của một lực 20 N theo phương nằm ngang thì vật chuyển động với gia tốc 0,2 m/. Bỏ qua ma sát giữa vật và mặt phẳng ngang.
a) Tính khối lượng của vật.
b) Tính quãng đường vật đi được khi vật đạt vận tốc 18 m/s.
c) Nếu hệ số ma sát giữa vật và mặt phẳng ngang là 0,005. Tính gia tốc của vật khi tác dụng lực ở trên lên vật, lấy g = 10 m/.
Một canô chạy thẳng xuôi dòng từ bến A đến bến B cách nhau 36km mất một khoảng thời gian là 1 giờ 30 phút. Vận tốc của nước đối với bờ sông là 6 km/h.
a) Tính vận tốc của ca nô đối với nước.
b) Tính khoảng thời gian để canô chạy ngược dòng chảy từ bến B trở về bến A.
Phát biểu điều kiện cân bằng của một chất điểm và quy tắc hình bình hành khi tổng hợp hai lực đồng qui.
Sự rơi tự do là gì? Nêu các đặc điểm và công thức của sự rơi tự do.