A. x = 4cos(20t +\(\frac{\pi }{3}\)) (cm).
B. x = 4cos(20t +\(\frac{\pi }{3}\)) (cm).
C. x = 3cos(20t -\(\frac{\pi }{3}\)) (cm).
D. x = 3cos(20t -\(\frac{\pi }{3}\)) (cm).
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
+ Phương trình dao động của chất điểm có dạng: \[x = A\cos \left( {\omega t + \varphi } \right)\]
+ Chu kì dao động của chất điểm : \[T = \frac{t}{N} = \frac{{31,4}}{{100}} = \frac{\pi }{{10}}s\]
+ Tần số góc của dao động: \[\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\](rad/s)
+ Biên độ dao động của chất điểm:
\[{A^2} = {x^2} + {\left( {\frac{v}{\omega }} \right)^2} \Rightarrow A = \sqrt {0,{{02}^2} + \left( {\frac{{40\sqrt 3 {{.10}^{ - 2}}}}{{{{20}^2}}}} \right)} = 0,04m = 4cm\]
+ Tại t = 0, x = 2, v < 0 \[ \Rightarrow \varphi = \frac{\pi }{3}\]
Vậy phương trình dao động của vật là: \[x = 4\cos \left( {20t + \frac{\pi }{3}} \right)\](cm)
Chọn đáp án B
Một chất điểm thực hiện đồng thời hai dao động có phương trình li độ lần lượt là ![]() và
và 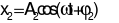 . Biên độ dao động tổng hợp A được tính bằng biểu thức
. Biên độ dao động tổng hợp A được tính bằng biểu thức
 , hai đầu cố định. Sóng dừng trên dây có bước sóng dài nhất là
, hai đầu cố định. Sóng dừng trên dây có bước sóng dài nhất là