Chứng minh rằng A chia hết cho 21.
Giải bởi qa.haylamdo.com
Lời giải:
A = 1 + 4 + 42+ 43+ … + 41999+ 42000
= (1 + 4 + 42) + (43+ 44+ 45) + … + (41998+ 41999+ 42000)
= 21 + 43.(1 + 4 + 42) + … + 41998.(1 + 4 + 42)
= 21 + 43.21 + … + 41998.21
= 21.(1 + 43+ … + 41998)
Vì 21 ⁝ 21 nên theo tính chất chia hết của một tích thì
21.(1 + 43+ … + 41998) ⁝ 21.
Vậy A ⁝ 21.
a) 126 + 73 + 174 + 127
b) 21.55 + 45.21
c) 400 : [121 – (27 – 6)]
a) x + 23 = 48
b) 8 + 2.(x – 4) = 20
c) 3x – 8 = 26: 24
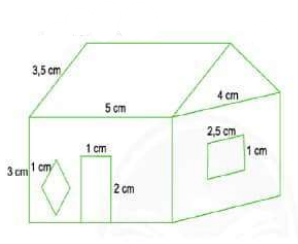
Trong hình vẽ bên có các hình:
