Giải bởi qa.haylamdo.com
Lời giải:
Ta có: n2+ n + 1 = (n . n + n) + 1 = n(n + 1) + 1
Vì n và n + 1 là hai số tự nhiên liên tiếp nên trong hai số n và n + 1, có một số là số chẵn.
TH1: n là số chẵn nên n ⁝ 2
Suy ra n(n + 1) ⁝ 2 (theo tính chất chia hết của một tích).
TH2: n + 1 là số chẵn nên (n + 1) ⁝ 2
Suy ra n(n + 1) ⁝ 2 (theo tính chất chia hết của một tích).
Do vậy trong mọi trường hợp thì n(n + 1) đều chia hết cho 2 nên nó là số chẵn, mà 1 là số lẻ nên n(n + 1) + 1 là số lẻ.
Vậy với mọi số tự nhiên n thì n2+ n + 1 là số lẻ.
a) 2x + 4 = 23
b) 3x + 1 + 23 = 2.52.20220
c) 180 ⁝ x và 12 < x ≤ 20
a) 38 + 53 + 62 + 57 + 22
b) 25.15 + 47.95 + 25.38 – 47.70
c) (23.93+ 92.45) : (92.15 – 2.92)
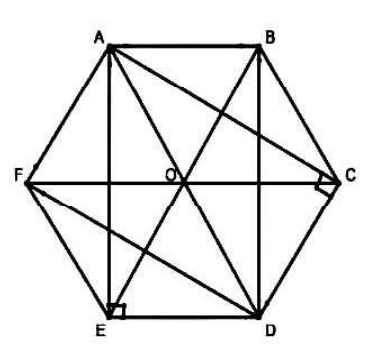
a) Kể tên 2 hình tam giác đều, 2 hình thoi, 2 hình chữ nhật có trong hình bên.
b) Tính tổng diện tích hình chữ nhật ABDE và hình thoi AOEF theo đơn vị mét vuông. Cho AB = 90 cm; AE = 156 cm.
