Ta có a, b phân biệt; nếu a // c và b // c thì:
A. \[a \bot b\];
B. \[a \equiv b\];
C. \[a \cap b\];
D. a // b.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: D
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Cho hai điểm phân biệt H, K. Ta vẽ một đường thẳng x đi qua điểm H và một đường thẳng y đi qua điểm K sao cho x // y. Có thể vẽ được bao nhiêu cặp đường thẳng x, y thỏa mãn điều kiện trên.
Điền cụm từ thích hợp vào chỗ trống: “Nếu một đường thẳng cắt hai đường thẳng … thì hai góc đồng vị bằng nhau.”
Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó.
Qua điểm M nằm ngoài đường thẳng a, ta vẽ ba đường thẳng qua M và song song với a thì:
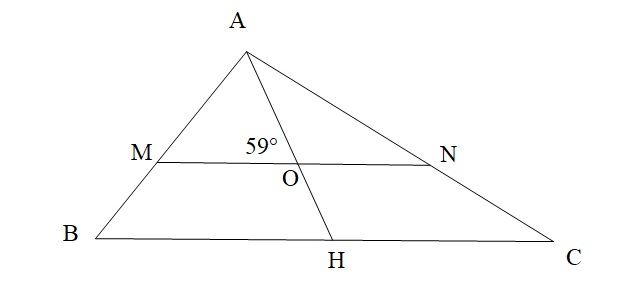
Cho hình vẽ bên dưới. Tính số đo góc OHC, biết MN // BC và \[\widehat {AOM} = 59^\circ \]
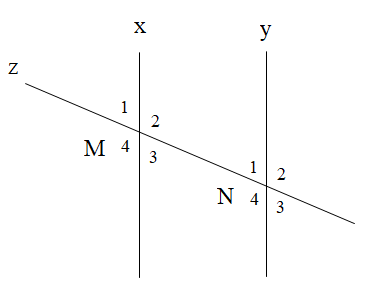
Cho hình vẽ như bên dưới. Tính \[\widehat {{M_3}}\], biết \[\widehat {{N_2}} = 137^\circ \].
Điền nội dung phù hợp vào chỗ trống: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng … với đường thẳng kia.”
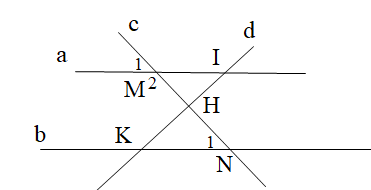
Cho hình vẽ bên dưới. Tính góc \[{M_2}\], biết a // b và \[{N_1} = 40^\circ \].
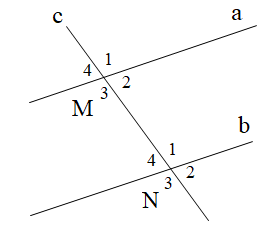
Cho hình vẽ như bên dưới. Tính \[\widehat {{N_3}}\], biết a // b và \[\widehat {{M_1}} = 50^\circ \].
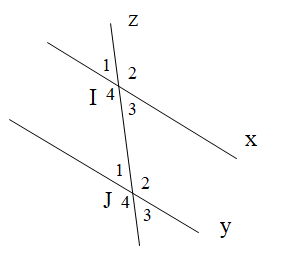
Cho hình vẽ bên dưới. Tính \[\widehat {{I_1}}\], biết \[\widehat {{J_3}} = 26^\circ \]và x // y.
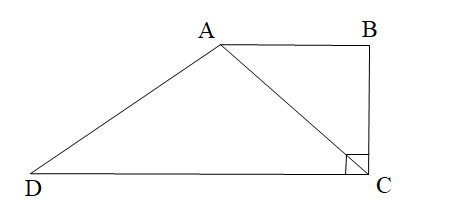
Cho hình thang ABCD như hình vẽ. Tính góc BAC, biết AC là tia phân giác góc BCD.
Nếu đường thẳng t cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì: