Chọn đáp án đúng.
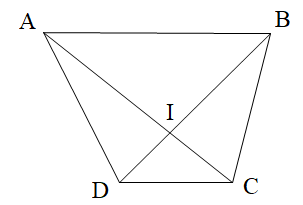
A. ^AIDvà ^CIB là hai góc kề bù;
B. ^ABC và ^ADC là hai góc kề bù;
C. ^AIB và ^BIC là hai góc kề bù;
D. ^AIB và ^DIC là hai góc kề bù.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: C
^AIDvà ^CIB là hai góc hai góc kề bù (sai, vì ^AIDvà ^CIB là hai góc hai góc đối đỉnh loại phương án A);
^ABC và ^ADC là hai góc kề bù (sai, vì ^ABC và ^ADC là hai góc của tứ giác ABCD, loại phương án B);
^AIB và ^BIC là hai góc kề bù (đúng, chọn phương án C);
^AIB và ^DIC là hai góc kề bù (sai, vì ^AIB và ^DIC là hai góc đối đỉnh, loại phương án D).
Cho các phát biểu sau:
(1) Tổng số đo hai góc kề nhau bằng 180o;
(2) Hai góc bằng nhau thì đối đỉnh;
(3) Hai đường thẳng song song thì cắt nhau;
(4) Hai góc kề bù có tổng số đo bằng 180o;
(5) Nếu NH = NK thì N là trung điểm của HK.
Có bao nhiêu phát biểu đúng?
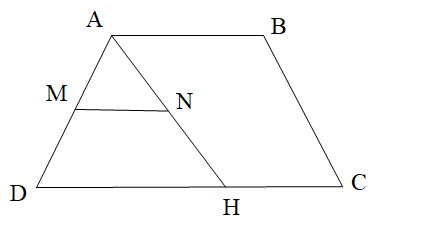
Cho hình thang ABCD như hình vẽ. Biết MN // DC, ^DAB=120∘ và ^ANM=40∘. Số đo góc AHD là:
Cho hai điểm phân biệt H, K. Ta vẽ một đường thẳng x đi qua điểm H và một đường thẳng y đi qua điểm K sao cho x // y. Có thể vẽ được bao nhiêu cặp đường thẳng x, y thỏa mãn điều kiện trên.
Cho hình vẽ,
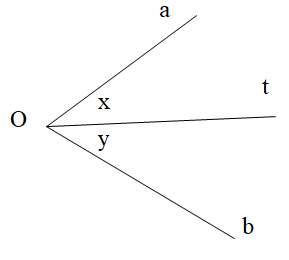
Biết ^aOb=70∘ và tia Ot là tia phân giác góc xOy. Tính x, y.
Hai đường thẳng mn và m’n’ cắt nhau tại điểm O. Góc đối đỉnh của ^mOn′ là:
Viết giả thiết, kết luận cho định lí sau:
“Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.”
Cho ^mOn và ^nOp là hai góc kề bù. Biết ^mOn=124∘ và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
Phát biểu định lí sau bằng lời.
Giả thiết | t cắt m tại A, t cắt n tại B ^A1 và ^B1là hai góc đồng vị ^A1=^B1 |
Kết luận | m // n |