Tính diện tích hình thoi \[MBND\]biết \[ABCD\] là hình vuông và hai đường chéo của hình vuông \[AC = BD = 20{\rm{ c}}m\]( \[M\]là điểm chính giữa AO; N là điểm chính giữa OC)
Giải bởi qa.haylamdo.com
Lời giải
Hai đường chéo hình vuông bằng nhau và cắt nhau tại trung điểm mỗi đường nên
\[OA = OC = 20:2 = 10(cm)\]
Vì điểm M, N là các điểm chính giữa của OA, OC nên:
\[OM = ON = OA:2 = 10:2 = 5(cm)\]
Do đó hình thoi \[MBND\] có độ dài đường chéo \[MN = 2.OM = 2.5 = 10(cm)\]
Đường chéo \[BD = 20(cm)\]
Diện tích hình thoi \[MBND\] là \[\frac{1}{2}MN.BD = \frac{1}{2}10.20 = 100(c{m^2})\]
Một mảnh vườn hình thoi có tổng hai đường chéo bằng \[71{\rm{ m}}\], đường chéo thứ nhất hơn đường chéo thứ hai \[10{\rm{ m}}\].
Tìm độ dài mỗi đường chéo.
Một mảnh vườn hình thoi có tổng độ dài hai đường chéo là \[220{\rm{ m}}\], biết đường chéo thứ nhất bằng \[\frac{2}{3}\]độ dài đường chéo thứ hai
Tính diện tích mảnh vườn đó.
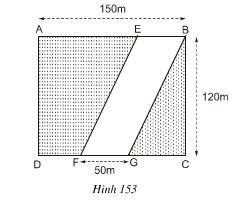
Người ta dành \[\frac{1}{{16}}\]diện tích mảnh vườn để làm nhà ở và vườn hoa. Tính diện tích để làm nhà ở và vườn hoa.
Tính diện tích hình thoi, biết:
