Cho tam giác ABC nhọn. Vẽ tia Ax nằm trong góc BAC, Ax cắt BC ở M. Gọi E và F theo thứ tự là hình chiếu của B và C trên tia Ax. So sánh BE + CF với BC.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: A
Hướng dẫn giải
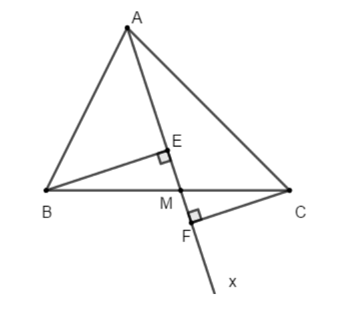
Vì BE ^ Ax tại E nên tam giác BEM vuông tại E.
Suy ra BM > BE (quan hệ đường xiên và đường vuông góc).
Vì CF ^ Ax tại F nên tam giác CFM vuông tại F.
Suy ra CM > CF (quan hệ đường xiên và đường vuông góc).
Khi đó ta có: BM + CM > BE + CF.
Mà BM + CM = BC (M thuộc BC).
Do đó BC > BE + CF hay BE + CF < BC.
Cho ba điểm A, B, C thẳng hàng và B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm M. So sánh MB và MC, MB và MA.
Cho đường thẳng d và điểm A không thuộc đường thẳng d. Chọn khẳng định sai.
Cho hình vẽ sau:
Em hãy chọn khẳng định sai trong các khẳng định sau.
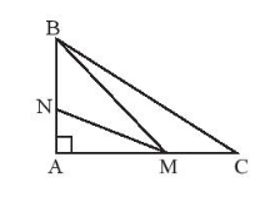
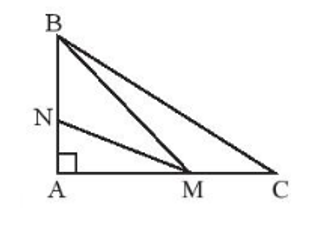
Quan sát hình dưới đây và cho biết đoạn ngắn nhất trong các đoạn BA, BM, BN, BC.
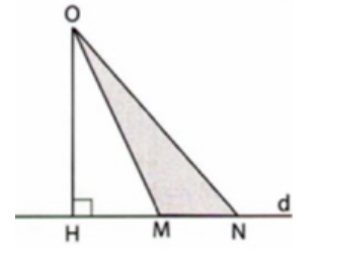
Quan sát hình bên dưới. Có các đường xiên và đường vuông góc kẻ từ O xuống đường thẳng c, trong số các đường này đường nào ngắn nhất?
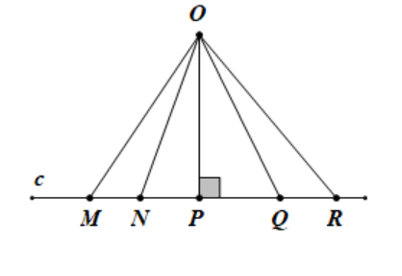
Em hãy chọn cụm từ thích hợp điền vào chỗ trống: "Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì ..."
Cho ba điểm A, B, C thẳng hàng và B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H. Khi đó:
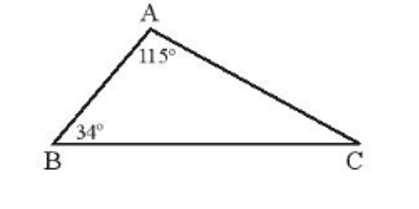
Quan sát hình vẽ bên dưới. Hãy so sánh hai cạnh CB và CA của tam giác ABC.
Quan sát hình dưới đây và cho biết đoạn ngắn nhất trong các đoạn MA, MB, MN, MC.