Cho tam giác ADK nhọn. Qua A kẻ đường thẳng song song với DK, qua D kẻ đường thẳng song song với AK, hai đường thẳng này cắt nhau tại B. Khẳng định nào sau đây là sai:
A. DABD = DDKA;
B. DABK = DDKB;
C. \(\widehat {BAK} = \widehat {BDA};\)
D. \(\widehat {ABD} = \widehat {AKD}.\)
Giải bởi qa.haylamdo.com
Đáp án đúng là: C
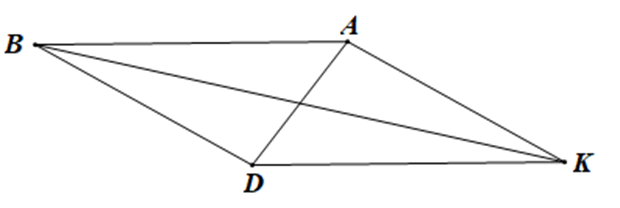
Vì AB // DK nên \(\widehat {BAD} = \widehat {KDA}\)(hai góc so le trong)
Vì DB // AK nên \(\widehat {KAD} = \widehat {BDA}\) (hai góc so le trong)
Xét DABD và DDKA có:
\(\widehat {BAD} = \widehat {KDA}\)(chứng minh trên),
AD là cạnh chung,
\(\widehat {BDA} = \widehat {KAD}\) (chứng minh trên)
Do đó DABD = DDKA (g.c.g)
Suy ra \(\widehat {ABD} = \widehat {DKA}\) (hai góc tương ứng)
Chứng minh tương tự ta cũng có: DABK = DDKB (g.c.g)
Suy ra \(\widehat {BAK} = \widehat {KDB}\) (hai góc tương ứng)
Vậy ta chọn phương án C.
Cho góc xOy khác góc bẹt. Trên tia phân giác của góc xOy lấy điểm M tuỳ ý, qua M vẽ đường thẳng vuông góc với OM, cắt Ox ở H và cắt Oy ở G. Khẳng định nào sau đây là đúng?
Cho hình vẽ dưới đây:
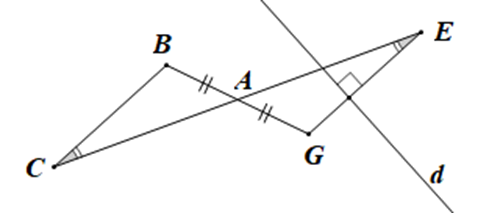
Xét các khẳng định:
(1) BC = EG;
(2) d ^ BC.
Chọn câu đúng:
Cho tứ giác ABCD, AB // DC, AB = DC, O là giao điểm của AC và BC. Khẳng định nào sau đây là đúng:
Cho hình vẽ dưới đây:
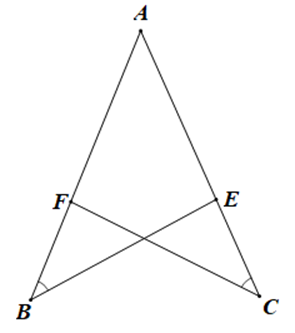
Biết \(\widehat {ABE} = \widehat {ACF}.\) Cần thêm điều kiện nào sau đây để DABE = DACF theo trường hợp góc – cạnh – góc:
Điền vào chỗ còn thiếu trong các bước chứng minh sau:
“Xét DABC và DADE có:
.............,
BC = DE.
\(\widehat {ABC} = \widehat {ADE};\)
Vậy ΔABC = ∆ADE (g.c.g)”
Cho DABC và DDEF có \(\widehat A = \widehat D,\widehat B = \widehat E.\) Để DABC = DDEF theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:
Cho tam giác DEG và tam giác HKI có \(\widehat D = \widehat K,\widehat E = \widehat I,\) DE = KI. Biết \(\widehat D + \widehat E = 100^\circ ,\) số đo góc H là:
