Cho các khẳng định sau:
(I). Mỗi góc chỉ có duy nhất một tia phân giác;
(II). Mỗi tia là tia phân giác của duy nhất một góc;
(III). Nếu tia Ot là tia phân giác của \(\widehat {aOb}\)thì Ot nằm giữa hai tia Oa và Ob;
(IV). Nếu \(\widehat {AOB}\)= \(\widehat {BOC}\) thì OB là tia phân giác của \(\widehat {AOC}\).
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
Giải bởi qa.haylamdo.com
Hướng dẫn giải:
Đáp án đúng là: A
+ Góc bẹt có hai tia phân giác.
Ví dụ: Cho \(\widehat {xOy}\) là góc bẹt. Khi đó Ot là tia phân giác của \(\widehat {xOy}\) và tia đối Oz của tia Ot cũng là tia phân giác của \(\widehat {xOy}\).
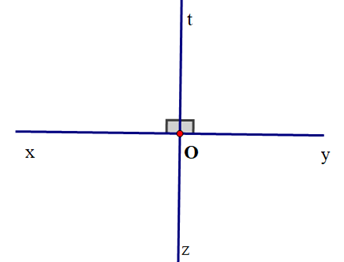
Do đó khẳng định (I) sai.
+ Mỗi tia có thể là tia phân giác của nhiều góc.
Ví dụ: Trong hình vẽ sau, Oc vừa là tia phân giác của \(\widehat {bOd}\), vừa là tia phân giác của \(\widehat {aOe}\).
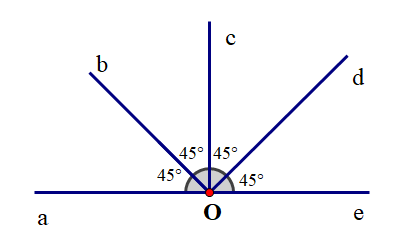
Do đó khẳng định (II) sai.
+ Nếu tia Ot là tia phân giác của \(\widehat {aOb}\)thì Ot nằm giữa hai tia Oa và Ob và \(\widehat {aOt} = \widehat {tOb}\).
Do đó khẳng định (III) đúng.
+ Nếu \(\widehat {AOB}\)= \(\widehat {BOC}\) thì OB chưa chắc là tia phân giác của \(\widehat {AOC}\).
Ví dụ: Trong hình vẽ sau, \(\widehat {AOB}\)= \(\widehat {BOC}\) nhưng tia OB không là tia phân giác của \(\widehat {AOC}\).
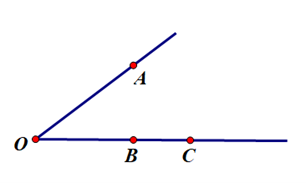
Do đó khẳng định (IV) sai.
Vậy chỉ có 1 khẳng định đúng trong các khẳng định trên.
Quan sát hình vẽ sau và cho biết tia Ob có là tia phân giác của \(\widehat {aOc}\) không? Vì sao?
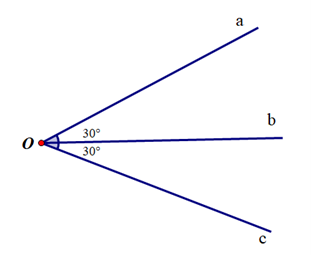
Cho \(\widehat {mOn} = {100^o}\) và các hình vẽ sau:
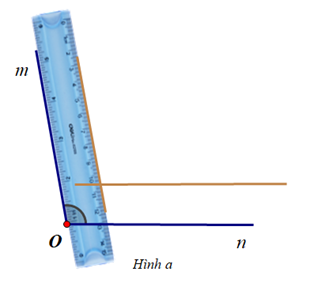
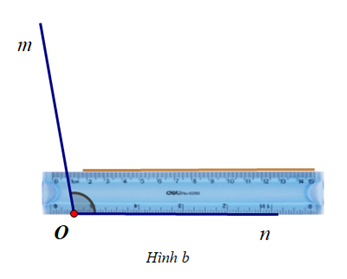
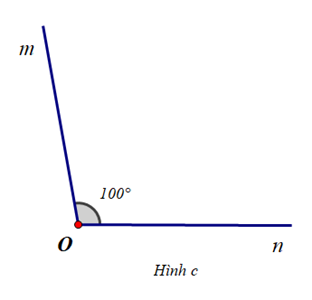
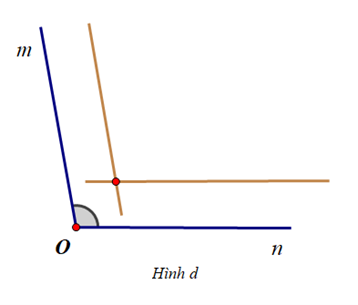
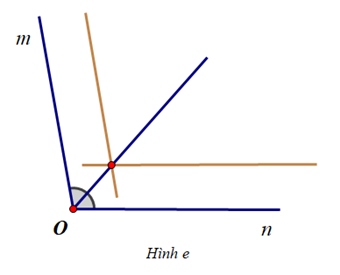
Trình tự nào sau đây thể hiện cách vẽ tia phân giác của \(\widehat {mOn}\)
Cho \(\widehat {xOy} = {120^o}\). Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng các cách sau đây:
Thước đo góc;
Cho \(\widehat {xOy} = {120^o}\). Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng các cách sau đây:
Compa.
Tia Ob là phân giác của \(\widehat {aOc}\) trong hình vẽ nào dưới đây?
Xét bài toán: "Cho \(\widehat {aOc} = {140^o}\). Nêu cách dựng tia phân giác của \(\widehat {aOc}\) bằng thước đo góc". Hãy sắp xếp một cách hợp lý các câu sau đây để có lời giải của bài toán trên.
(I). Tính \(\frac{{\widehat {aOc}}}{2} = \frac{{{{140}^o}}}{2} = {70^o}\).
(II). Dùng thước nối từ đỉnh của góc tới điểm đã đánh dấu ta được tia phân giác.
(III). Đặt tâm của thước đo góc trùng với đỉnh O sao cho một cạnh của thước đo trùng với cạnh Oc.
(IV). Dựng góc \(\widehat {aOc} = {140^o}\).
(V). Đánh dấu điểm chỉ vạch 70°.
Sắp xếp nào sau đây đúng?
Xét bài toán: "Cho \(\widehat {xOy} = {70^o}\). Nêu cách dựng tia phân giác của \(\widehat {xOy}\) bằng compa". Hãy sắp xếp một cách hợp lý các câu sau đây để có lời giải của bài toán trên.
(I). Dựng hai cung tròn tâm A và B có cùng bán kính sao cho chúng cắt nhau tại một điểm M nằm trong góc \(\widehat {xOy}\).
(II). Dựng góc \(\widehat {xOy} = {70^o}\).
(III). Vẽ tia OM, đó là tia phân giác của góc xOy cần dựng.
(IV). Dựng cung tròn tâm O bán kính tuỳ ý; cắt Ox, Oy lần lượt tại A và B.
Sắp xếp nào sau đây đúng?
Cho \(\widehat {xOy} = {120^o}\). Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng các cách sau đây:
Thước hai lề;
Cho tia Ob nằm giữa hai tia Oa và Oc; \(\widehat {aOb} = \widehat {bOc} = {20^o}\). Khẳng định nào sau đây sai?
