Cho hình hộp chữ nhật ABCD. EFGH. Chọn khẳng định đúng:
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là B
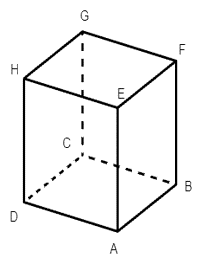
Vì ABCD. EFGH là hình hộp chữ nhật nên ta có:
• AEFB là hình chữ nhật suy ra AE // BF.
Do đó AE và BF không cắt nhau. Vậy A là một khẳng định sai.
• AEHD là hình chữ nhật mà ED và HA là hai đường chéo của hình chữ nhật này nên ED và HA cắt nhau. Vậy B là một khẳng định đúng.
• EFGH là hình chữ nhật suy ra EF // GH.
Do đó EF và GH không cắt nhau. Vậy C là một khẳng định sai.
• ABCD là hình chữ nhật suy ra AD // BC.
Do đó AD và BC không cắt nhau. Vậy D là một khẳng định sai.
Ta chọn đáp án B.
Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm,
AE = 4 cm. Khẳng định đúng là:
Cho hình hộp chữ nhật ABCD. EFGH. Có bao nhiêu cạnh song song với cạnh AE?
Cho hình hộp chữ nhật ABCD. A'B'C'D'. Biết AB = 2 cm. Độ dài cạnh CD và C'D' là
Cho hình hộp chữ nhật ABCD.A'B'C'D' có ba kích thước khác nhau. Cạnh có độ dài bằng cạnh AA' là:
