Hình lăng trụ đứng tứ giác có:
(1) Các mặt đáy song song với nhau;
(2) Các mặt đáy là tam giác;
(3) Các mặt đáy là tứ giác;
(4) Các mặt bên là hình chữ nhật.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: C
Hình lăng trụ đứng tứ giác có các mặt đáy là tứ giác và song song với nhau, các mặt bên là các hình chữ nhật.
Do đó (1) (3) (4) đúng.
Vậy có 3 khẳng định đúng.
Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước 4 cm, 9 cm. Chiều cao của lăng trụ đứng là 3 cm. Diện tích tất cả các mặt của hình lăng trụ đứng đó là:
Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:
Cho hình lăng trụ đứng ABCD.EHGF có đáy ABCD là hình thang cân (AB // CD). Có bao nhiêu cạnh có độ dài bằng với độ dài cạnh GH?
Cho một hình lăng trụ đứng có tổng 12 cạnh. Hỏi đáy của hình lăng trụ đứng này không thể là hình gì?
Cho hình lăng trụ đứng có diện tích xung quanh bằng 168 cm2, chiều cao 7 cm. Khi đó, chu vi đáy của hình lăng trụ đứng là:
Cho một hình khối như hình vẽ dưới đây:
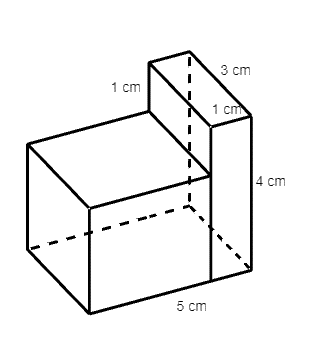
Thể tích hình khối trên là:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại A có chiều cao bằng 4 cm. Biết hai cạnh góc vuông của tam giác đáy bằng nhau và bằng một nửa cạnh bên của lăng trụ đó. Thể tích của lăng trụ bằng