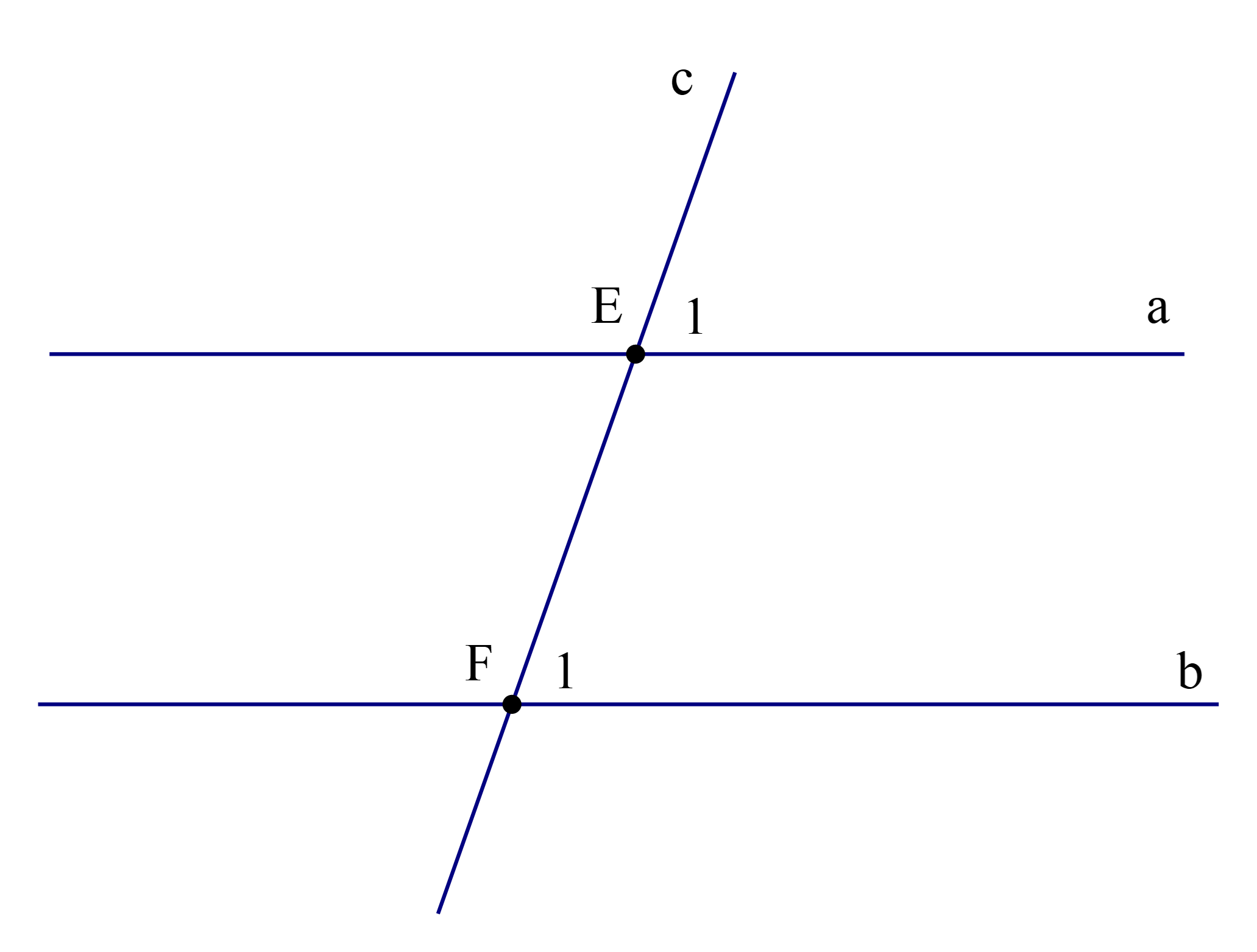
Một định lí được minh họa bởi hình vẽ:
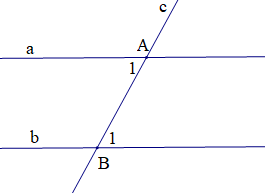
Định lí có giả thiết và kết luận như sau:
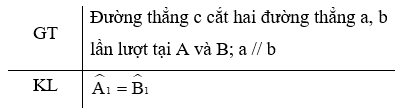
Định lí được phát biểu thành lời là:
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: C
Từ giả thiết và kết luận ta có: Nếu đường thẳng c cắt hai đường thẳng song song a và b lần lượt tại hai điểm A và B thì hai góc so le trong \({\widehat A_1}\) và \({\widehat B_1}\) bằng nhau.
Một cách tổng quát ta có định lí: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.
Vậy ta chọn phương án C.
Cho định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”. Giả thiết của định lí là
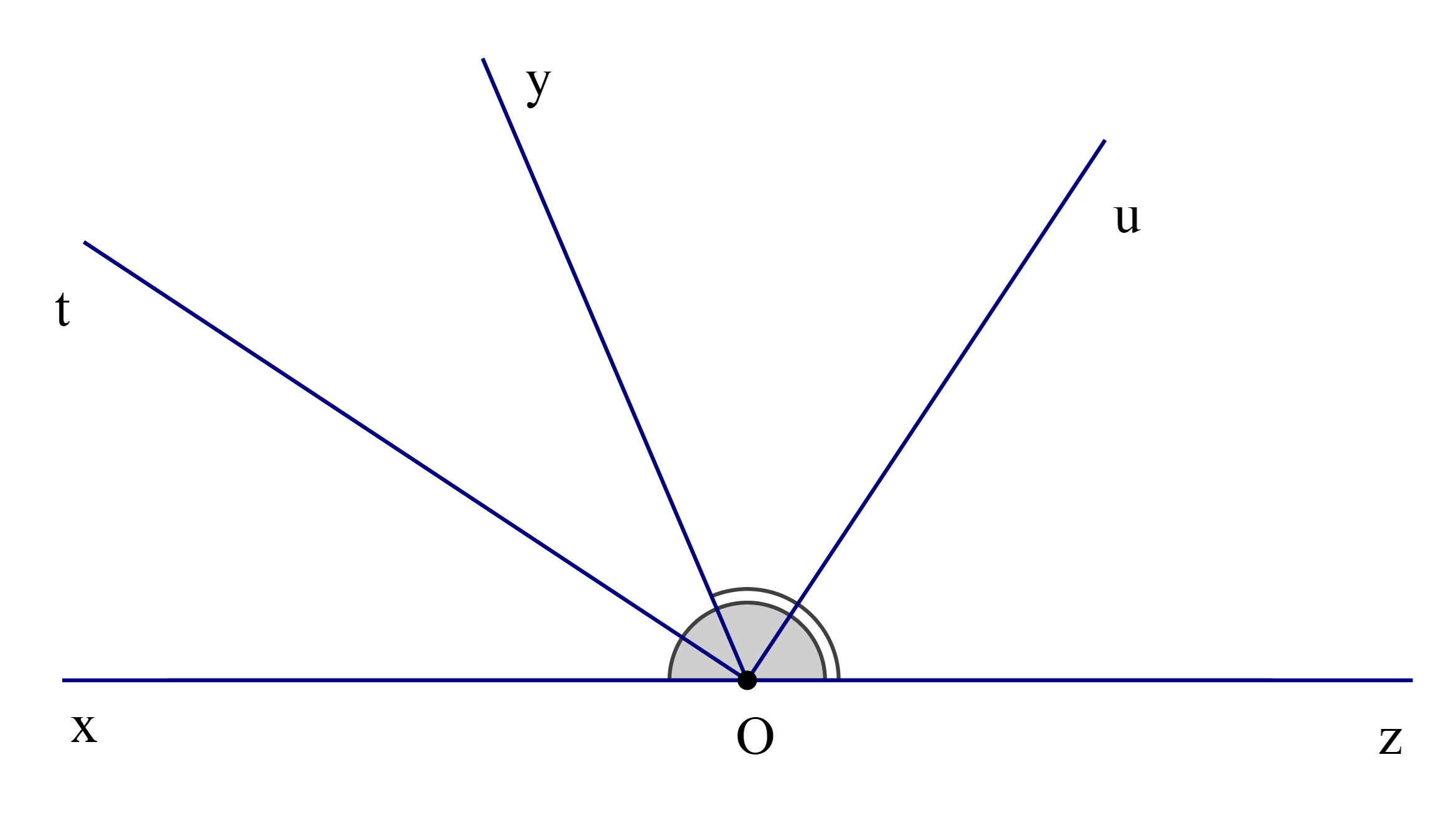
Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau”. Kết luận của định lí là
Cho giả thiết: “Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba”. Kết luận nào dưới đây là đúng để được một định lí hoàn chỉnh:
Cho các khẳng định sau:
(1) Nếu hai đường thẳng song song thì không có điểm chung.
(2) Nếu hai đường thẳng cắt nhau thì vuông góc.
(3) Nếu hai đường thẳng có điểm chung thì cắt nhau.
(4) Nếu OA = OB thì O là trung điểm của AB.
Có bao nhiêu khẳng định là định lí?
Phần giả thiết: c cắt a tại điểm E, c cắt b tại điểm F và \({\widehat {\rm{E}}_1} = {\widehat {\rm{F}}_1}\) (như hình vẽ) là của định lí nào sau đây?
Cho định lí: “Hai tia phân giác của hai góc kề bù thì tạo thành một góc vuông” được minh họa bởi hình vẽ dưới đây:
Kết luận của định lí là:
