Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
c. So sánh ∠(BAM) và ∠(MAC)
Giải bởi qa.haylamdo.com
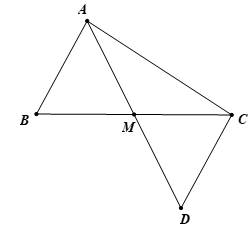
c. Trong tam giác ADC có CD < AC ⇒ ∠(DAC) < ∠(ADC) (1 điểm)
Mà ∠(BAM) = ∠(ADC) ( 2 góc tương ứng vì ΔABM = ΔDCM) (0.5 điểm)
Suy ra ∠(MAB) > ∠(MAC) (0.5 điểm)
B. Phần tự luận (6 điểm)
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
a. Chứng minh ΔAMB = ΔDMC
A. Phần trắc nghiệm (4 điểm)
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Cho tam giác ABC có độ dài các cạnh Góc lớn nhất của tam giác là:
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
b. Chứng minh AC > CD
Cho tam giác ABC có độ dài các cạnh So sánh các góc của tam giác ABC.
Tam giác cân có độ dài hai cạnh là 3cm, 7cm. Khi đó độ dài cạnh còn lại là:
