Đề kiểm tra 15 phút Toán 7 Chương 3 Hình học có đáp án (phần Qhgcytttg - Trắc nghiệm - Tự luận 4)
-
10474 lượt thi
-
7 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
A. Phần trắc nghiệm (4 điểm)
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Cho tam giác ABC có độ dài các cạnh Góc lớn nhất của tam giác là:
Vì cạnh AB là cạnh lớn nhất nên góc C là góc lớn nhất. Chọn C
Câu 2:
Tam giác cân có độ dài hai cạnh là 3cm, 7cm. Khi đó độ dài cạnh còn lại là:
Theo bất đẳng thức tam giác, cạnh còn lại lớn hơn 4cm và nhỏ hơn 10cm mà tam giác là tam giác cân nên chọn C
Câu 3:
Cho tam giác ABC có Cạnh lớn nhất của tam giác là:
Tam giác ABC là tam giác vuông nên góc A là góc lớn nhất, suy ra cạnh lớn nhất là BC. Chọn B
Câu 4:
Cho tam giác ABC có độ dài các cạnh So sánh các góc của tam giác ABC.
Vì BC < AC < AB ⇒ ∠A < ∠B < ∠C hay ∠C > ∠B > ∠A . Chọn D
Câu 5:
B. Phần tự luận (6 điểm)
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
a. Chứng minh ΔAMB = ΔDMC
a. Hình vẽ (1 điểm)
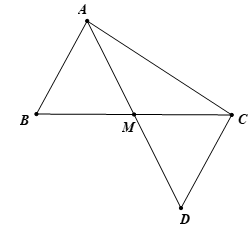
Xét ΔABM và ΔBCM có:
BM = MC
∠(AMB) = ∠(BMC)
AM = MD
⇒ ΔABM = ΔBCM (c.g.c) (1 điểm)
Câu 6:
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
b. Chứng minh AC > CD
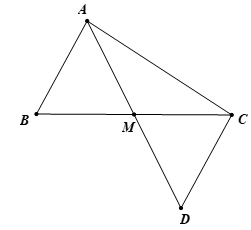
b. Vì ΔABM = ΔBCM ⇒ AB = DC mà AB < AC ⇒ CD < AC (2 điểm)
Câu 7:
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
c. So sánh ∠(BAM) và ∠(MAC)
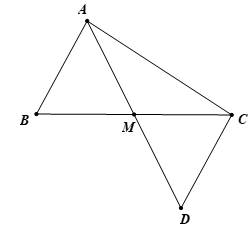
c. Trong tam giác ADC có CD < AC ⇒ ∠(DAC) < ∠(ADC) (1 điểm)
Mà ∠(BAM) = ∠(ADC) ( 2 góc tương ứng vì ΔABM = ΔDCM) (0.5 điểm)
Suy ra ∠(MAB) > ∠(MAC) (0.5 điểm)
