Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
b. Tính góc (AIB)
Giải bởi qa.haylamdo.com
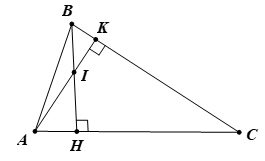
b. Trong tam giác vuông ABH có ∠(ABH) + ∠(AHB) + ∠(BAH) = 180o
Nên ∠(ABH) = 180o - 60o - 90o = 30o ( 1 điểm)
Trong tam giác vuông ABK có (BAK) + (ABK) + (BKA) = 180o
Nên ∠(BAH) = 180o - 70o - 90o = 20o ( 1 điểm)
Trong tam giác ABM có ∠(ABI) + ∠(BAI) + ∠(IAB) = 180onên
∠(AMB) = 180o - 20o - 30o = 130o ( 1 điểm)
Cho đoạn thẳng AB, d là đường trung trực của AB. Khẳng định nào sau đây là sai:
Cho tam giác ABC nhọn có I là giao điểm của hai đường cao kẻ từ B và C. Khi đó AI là:
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
a. So sánh các cạnh của tam giác ABC
A. Phần trắc nghiệm (4 điểm)
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Giao điểm của ba đường trung tuyến trong tam giác được gọi là:
Cho tam giác ABC có góc Các tia phân giác cắt nhau tại E. Khi đó số đo góc (ACE) là:
