Phát biểu đúng là
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: A
Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.
Cho tam giác ABC và tam giác DEF có AB = DE, AC = DF, \(\widehat A = \widehat D\). Biết \(\widehat B = 60^\circ \). Số đo góc E là
Cho tam giác ABC và tam giác MNP có \(\widehat A = \widehat P\); AB = PN, AC = PM. Phát biểu nào sau đây đúng?
Cho tam giác ABC và tam giác \[NPM\] có BC = PM; \(\widehat B = \widehat P\). Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp góc – cạnh – góc?
Cho tam giác ABC và tam giác MNP có \(\widehat A = \widehat P\); AC = MP, \[\widehat C = \widehat M\]. Phát biểu nào sau đây đúng?
Cho tứ giác ABCD, \[AB{\rm{//}}DC\], \[AD{\rm{//}}BC\], O là giao của AC và BD. Câu nào sau đây đúng?
Cho hình vẽ dưới đây, biết CE = DE và \(\widehat {CEA} = \widehat {DEA}\).
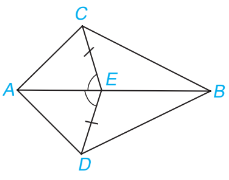
Khẳng định sai là
Cho \[\Delta DEF\] có \(\widehat E = \widehat F\). Tia phân giác của góc D cắt EF tại I. Ta có
Cho tam giác ABC và tam giác \[NPM\] có BC = PM; \(\widehat B = \widehat P\). Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh?
Cho tam giác ABC và tam giác DEF có AB = DE, \(\widehat B = \widehat E,{\rm{ }}\widehat A = \widehat D\). Biết AC = 6 cm. Độ dài DF là
Cho góc xOy khác góc bẹt. Trên tia phân giác của góc xOy lấy điểm I tùy ý, qua I vẽ đường thẳng vuông góc với OI cắt Ox ở E và cắt Oy ở F. Trong các khẳng định sau, khẳng định nào đúng?
Cho hình vẽ sau, trong đó \(AB{\rm{//}}CD\), AB = CD. Khẳng định đúng là
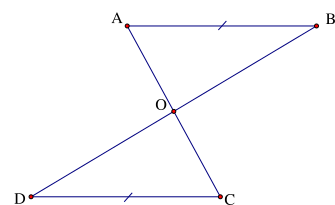
Cho hình vẽ dưới đây, biết đoạn thẳng JK song song và bằng đoạn thẳng ML.
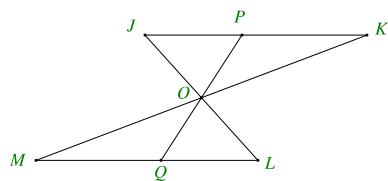
Khẳng định đúng là