Cho ΔABC cân tại A, AB = AC = 5 cm; BC = 8 cm. Kẻ AH⊥BC (H∈BC).
a) Chứng minh HB = HC.
b) Tính AH.
c) Kẻ HD⊥AB (D∈AB); HE⊥AC (E∈AC). Chứng minh: ΔHDE là tam giác cân.
Giải bởi qa.haylamdo.com
|
GT |
ΔABC cân tại A, AB = AC = 5 cm; BC = 8 cm. AH⊥BC (H∈BC); HD⊥AB (D∈AB); HE⊥AC (E∈AC). |
|
KL |
a) Chứng minh HB = HC. b) Tính AH. c) ΔHDE là tam giác cân. |
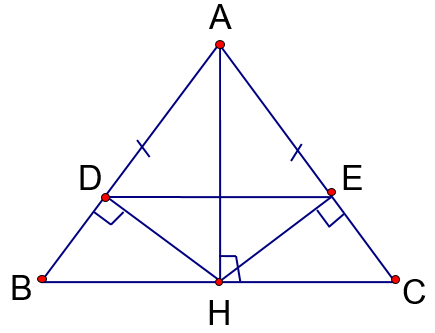
a) Xét ∆ABH và ∆ACH có:
^AHB=^AHC=90o
AB = AC = 5 cm
Cạnh AH chung
Do đó ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông)
Suy ra BH = CH (hai cạnh tương ứng)
b) Từ câu a: BH = CH suy ra BH=BC2=82=4(cm).
Áp dụng định lý Py-ta-go vào ∆AHB vuông tại H, ta có:
AB2 = AH2 + BH2
⇒ AH2 = AB2 − BH2 = 52 − 42 = 25 – 16 = 9.
Do đó AH=√9=3(cm)
c) Xét ∆DBH và ∆ECH có:
ˆB=ˆC (vì ∆ABC cân tại A)
BH = CH (cmt)
^BDH=^HEC=90o
Do đó ∆ABH = ∆ACH (cạnh huyền – góc nhọn)
Suy ra DH = EH (hai cạnh tương ứng).
Vậy ∆DHE cân tại H.
Trên tia phân giác góc A của tam giác ABC (AB > AC) lấy điểm M. Chứng minh |MB – MC| < AB – AC.
Cho đơn thức: A = (2x2y3).(−3x3y4)
a) Thu gọn đơn thức A.
b) Xác định hệ số và bậc của đơn thức A sau khi đã thu gọn.
Điểm kiểm tra cuối học kì I môn vật lý của lớp 7A được bạn lớp trưởng ghi lại như sau:
|
5 |
8 |
4 |
8 |
6 |
6 |
5 |
7 |
4 |
3 |
6 |
7 |
|
7 |
3 |
8 |
6 |
7 |
6 |
5 |
9 |
7 |
9 |
7 |
4 |
|
4 |
7 |
10 |
6 |
7 |
5 |
4 |
7 |
6 |
5 |
2 |
8 |
a) Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b) Lập bảng “tần số” và tìm mốt của dấu hiệu.
c) Tính số trung bình cộng của dấu hiệu.
