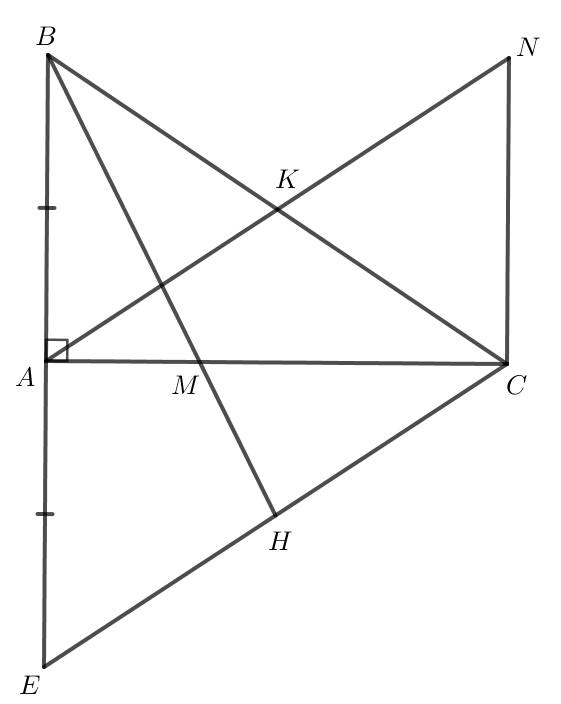
Cho tam giác ABC vuông tại A, AB = 9 cm, BC = 15 cm. Trên tia đối của tia AB lấy điểm E sao cho A là trung điểm của BE.
a) Chứng minh rằng
b) Vẽ đường trung tuyến BH của cắt cạnh AC tại M. Chứng minh M là trọng tâm của và tính độ dài đoạn CM.
c) Từ A vẽ đường thẳng song song với EC, đường thẳng này cắt cạnh BC tại K. Chứng minh rằng ba điểm E, M, K thẳng hàng.
Giải bởi qa.haylamdo.com
a) Xét vuông tại A và vuông tại A có:
AB = AE (theo giả thiết)
AC chung
(2 cạnh góc vuông)
b) Do A là trung điểm của BE nên CA là đường trung tuyến ứng của
Xét có CA và BH là hai đường trung tuyến cắt nhau tại M.
Do đó M là trọng tâm của
Do đó CM = 
CA.
Áp dụng định lý Pytago vào vuông tại A:
AB2 + AC2 = BC2
92 + AC2 = 152
AC2 = 225 - 81
AC2 = 144
AC = 12 cm
Khi đó CM = CA = .12 = 8 cm.
Vậy CM = 8 cm.
c) Trên tia đối của tia KA lấy điểm N sao cho KN = KA.
Do (2 cạnh góc vuông) nên BC = EC (2 cạnh tương ứng) và (2 góc tương ứng).
.
Do AK // EC nên (2 góc so le trong)
Do đó .
có nên cân tại K.
Do đó KA = KC.
Mà KA = KN = 
AN nên KA = KN = KC = AN.
có KA = KN = KC = AN nên vuông tại C.
Xét vuông tại C và vuông tại A:
(chứng minh trên).
AC chung.
(góc nhọn - cạnh góc vuông).
AN = CE (2 cạnh tương ứng).
Mà EC = BC nên AN = BC.
Mà AN = 2AK nên BC = 2AK.
Lại có AK = KC nên BC = 2KC.
Do đó K là trung điểm của BC.
có M là trọng tâm, lại có K là trung điểm của BC nên E, M, K thẳng hàng.
Vậy E, M, K thẳng hàng.
Cho hai đa thức:
f(x) = -6x3 - x4 + 3x2 + 2x4 - x - x2 + 1 và g(x) = 2x3 - x + x2 + x3.
a) Thu gọn và sắp xếp các hạng tử của 2 đa thức theo lũy thừa giảm dần của biến.
b) Tìm bậc, hệ số cao nhất, hệ số tự do của f(x) và g(x).
c) Tính h(x) = g(x) - f(x) và h(-1).
Cho ba số thực x, y, z thỏa mãn x(x2 + y) - yz = 0.
Biết rằng trong ba số đó có một số bằng 0, một số âm, một số dương. Hãy chỉ rõ số nào bằng 0, số nào âm, số nào dương.
Tìm nghiệm của các đa thức sau:
a) M = 2x - 
b) N = (x + 5)(4x2 - 1).
c) P = 9x3 - 25x.
Cho hai đa thức P(x) = -x3 + 2x2 + x - 1 và Q(x) = x3 - x2 - x + 2. Nghiệm của đa thức P(x) + Q(x) là:
