Cho các thông số như hình vẽ, Ot là tia phân giác góc zOx. Tính số đo góc zOt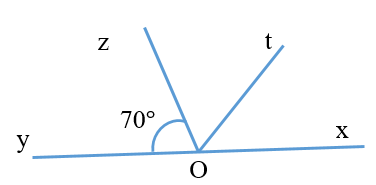
A. 65°;
B. 40°;
C. 55°;
D. 110°.
Giải bởi qa.haylamdo.com
Đáp án đúng là: C
Ta có: góc yOz và góc zOx là hai góc kề bù \[ \Rightarrow \widehat {yOz} + \widehat {zOx} = 180^\circ \]
\[ \Rightarrow \widehat {zOx} = 180^\circ - \widehat {yOz} = 180^\circ - 70^\circ = 110^\circ \]
Mà Ot là tia phân giác của góc zOx nên \[ \Rightarrow \widehat {zOt} = \widehat {xOt} = \frac{{\widehat {zOx}}}{2} = \frac{{110^\circ }}{2} = 55^\circ \]
Cho \(\widehat {xOy} = 120^\circ \), tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:
Cho \[\widehat {HOK} = 90^\circ \] và vẽ tia OI sao cho tia OK là tia phân giác của góc HOI. Khi đó góc HOI là:
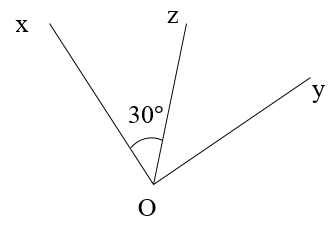
Tính số đo của góc xOy. Biết \[\widehat {xOz} = 30^\circ \], Oz là tia phân giác của góc xOy.
Cho . Vẽ tia OB sao cho OA là tia phân giác góc BOC. Tính số đo góc và .
Điền nội dung thích hợp vào chỗ trống.
“Đường thẳng chứa tia phân giác của một góc là ….”
Cho \[\widehat {aOb} = 80^\circ \], Ot là tia phân giác góc aOb. Số đo góc aOt là:
Tính góc xOt, biết góc xOy và góc x’Oy’ là hai góc đối đỉnh, và tia Ot là tia phân giác góc xOy.
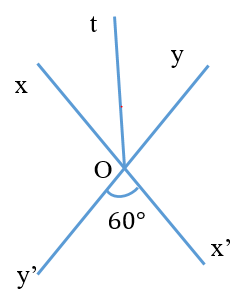
Cho tia Oz nằm trong góc xOy, \[\widehat {xOz} = \widehat {yOz}\] thì
