Cho \[\widehat {aOb} = 80^\circ \], Ot là tia phân giác góc aOb. Số đo góc aOt là:
A. 44°;
B. 40°;
C. 60°;
D. 64°.
Giải bởi qa.haylamdo.com
Đáp án đúng là: B
Ta có: Ot là tia phân giác góc aOb nên \[ \Rightarrow \widehat {aOt} = \widehat {bOt} = \frac{{\widehat {aOb}}}{2} = \frac{{80^\circ }}{2} = 40^\circ \].
Vậy số đo của góc aOt là 40°.
Cho \(\widehat {xOy} = 120^\circ \), tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:
Cho \[\widehat {HOK} = 90^\circ \] và vẽ tia OI sao cho tia OK là tia phân giác của góc HOI. Khi đó góc HOI là:
Cho các thông số như hình vẽ, Ot là tia phân giác góc zOx. Tính số đo góc zOt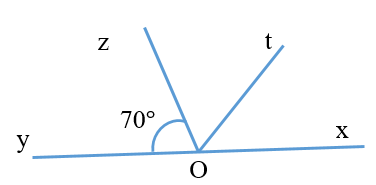
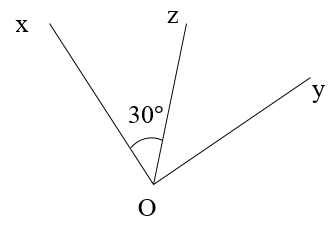
Tính số đo của góc xOy. Biết \[\widehat {xOz} = 30^\circ \], Oz là tia phân giác của góc xOy.
Cho . Vẽ tia OB sao cho OA là tia phân giác góc BOC. Tính số đo góc và .
Điền nội dung thích hợp vào chỗ trống.
“Đường thẳng chứa tia phân giác của một góc là ….”
Tính góc xOt, biết góc xOy và góc x’Oy’ là hai góc đối đỉnh, và tia Ot là tia phân giác góc xOy.
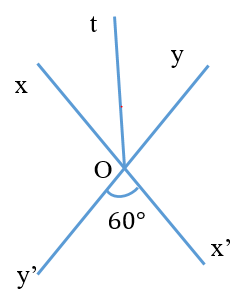
Cho tia Oz nằm trong góc xOy, \[\widehat {xOz} = \widehat {yOz}\] thì
