Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo AC và BD sao cho ^AOB=2^AOD=4^ODC. Chọn khẳng định đúng:
Giải bởi qa.haylamdo.com
Hướng dẫn giải:
Đáp án đúng là: C
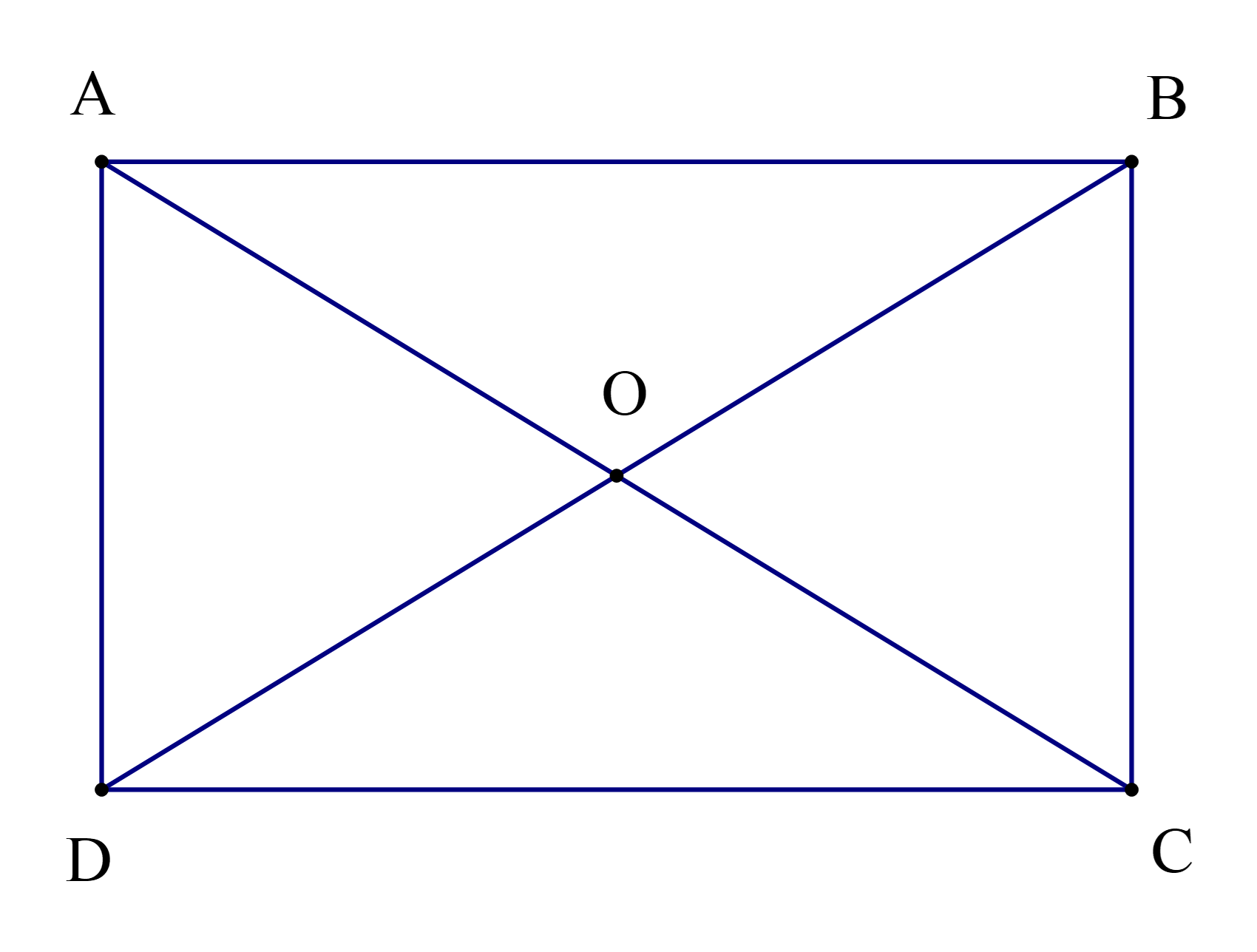
Theo bài ta có 2^AOD=4^ODC.
Suy ra ^AOD=2^ODC.
Vì hai góc ^AODv\`a^AOB là hai góc kề bù nên:
^AOD+^AOB=180∘
Hay 2^ODC+4^ODC=180∘ (vì ^AOD=2^ODC và ^AOB=4^ODC)
Suy ra 6^ODC=180∘
Suy ra ^ODC=180∘6=30∘
Ta lại có ABCD là hình chữ nhật do đó ^ADC=90∘
Mà ^ADO+^ODC=^ADC (hai góc kề nhau)
Suy ra ^ADO+^ODC=90∘
Hay ^ADO+30∘=90∘
Suy ra ^ADO=90∘−30∘=60∘
Vậy ^ADO=60∘.
Cho hình vẽ.
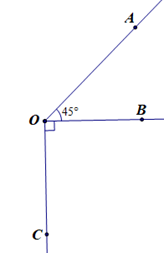
Kẻ tia OE là tia đối của tia OB và tia OD nằm giữa hai tia OC và OE sao cho ^COD=^DOE. Chọn khẳng định sai:
