Trắc nghiệm Toán 7 Bài 1. Các góc ở vị trí đặc biệt có đáp án (Vận dụng)
-
684 lượt thi
-
3 câu hỏi
-
15 phút
Danh sách câu hỏi
Câu 1:
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo AC và BD sao cho \(\widehat {{\rm{AOB}}} = 2\widehat {{\rm{AOD}}} = 4\widehat {{\rm{ODC}}}\). Chọn khẳng định đúng:
Hướng dẫn giải:
Đáp án đúng là: C
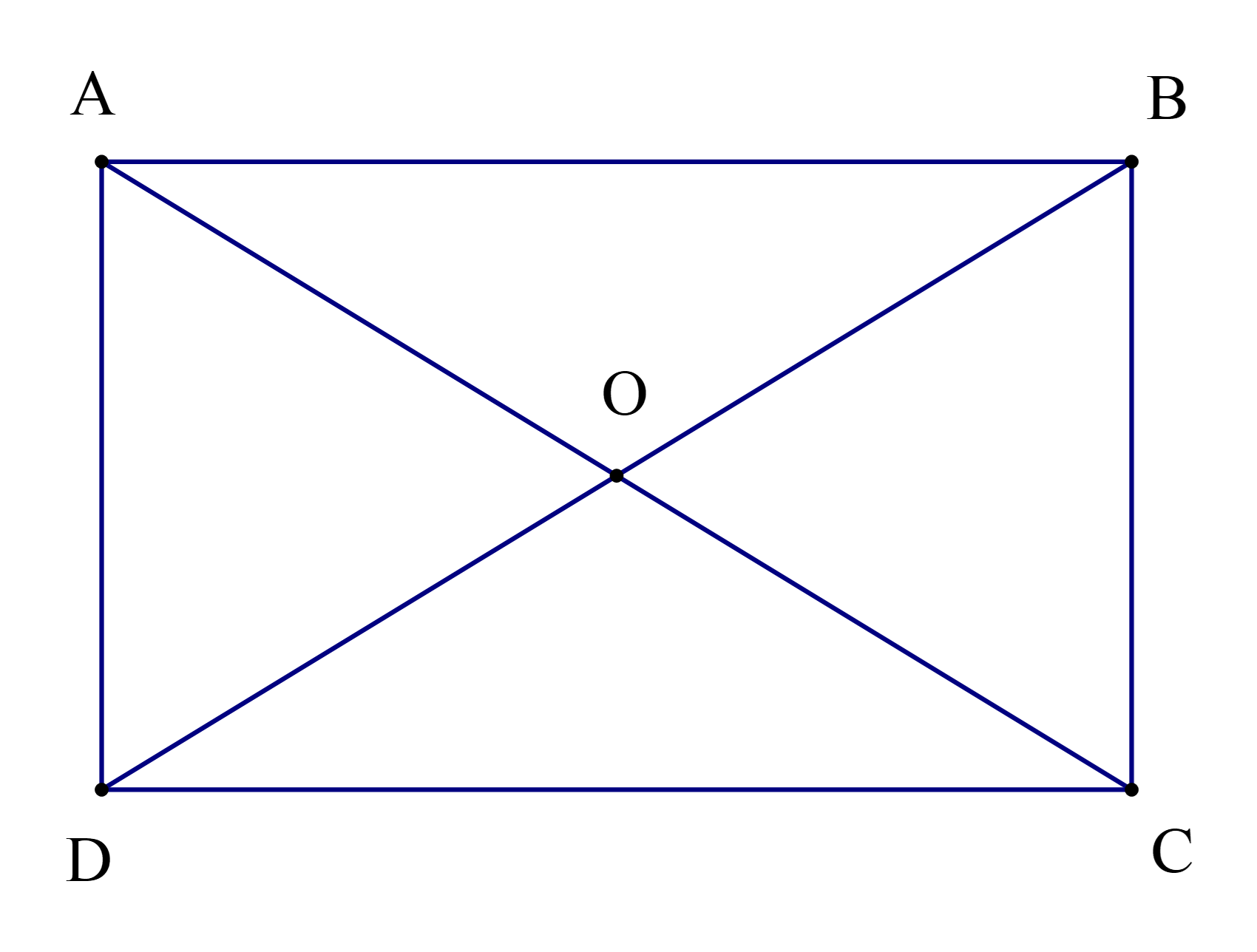
Theo bài ta có \(2\widehat {{\rm{AOD}}} = 4\widehat {{\rm{ODC}}}.\)
Suy ra \(\widehat {{\rm{AOD}}} = 2\widehat {{\rm{ODC}}}.\)
Vì hai góc \(\widehat {{\rm{AOD}}}{\rm{ v\`a }}\widehat {{\rm{AOB}}}\) là hai góc kề bù nên:
\(\widehat {{\rm{AOD}}} + \widehat {{\rm{AOB}}} = 180^\circ \)
Hay \(2\widehat {{\rm{ODC}}} + 4\widehat {{\rm{ODC}}} = 180^\circ \) (vì \(\widehat {{\rm{AOD}}} = 2\widehat {{\rm{ODC}}}\) và \(\widehat {{\rm{AOB}}} = 4\widehat {{\rm{ODC}}}\))
Suy ra \(6\widehat {{\rm{ODC}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{ODC}}} = \frac{{180^\circ }}{6} = 30^\circ \)
Ta lại có ABCD là hình chữ nhật do đó \(\widehat {{\rm{ADC}}} = 90^\circ \)
Mà \(\widehat {{\rm{ADO}}} + \widehat {{\rm{ODC}}} = \widehat {{\rm{ADC}}}\) (hai góc kề nhau)
Suy ra \(\widehat {{\rm{ADO}}} + \widehat {{\rm{ODC}}} = 90^\circ \)
Hay \(\widehat {{\rm{ADO}}} + 30^\circ = 90^\circ \)
Suy ra \(\widehat {ADO} = 90^\circ - 30^\circ = 60^\circ \)
Vậy \(\widehat {{\rm{ADO}}} = 60^\circ \).
Câu 2:
Cho hình vẽ, biết rằng \(\widehat {{\rm{AMC}}} - \widehat {{\rm{AMB}}} = 80^\circ \).
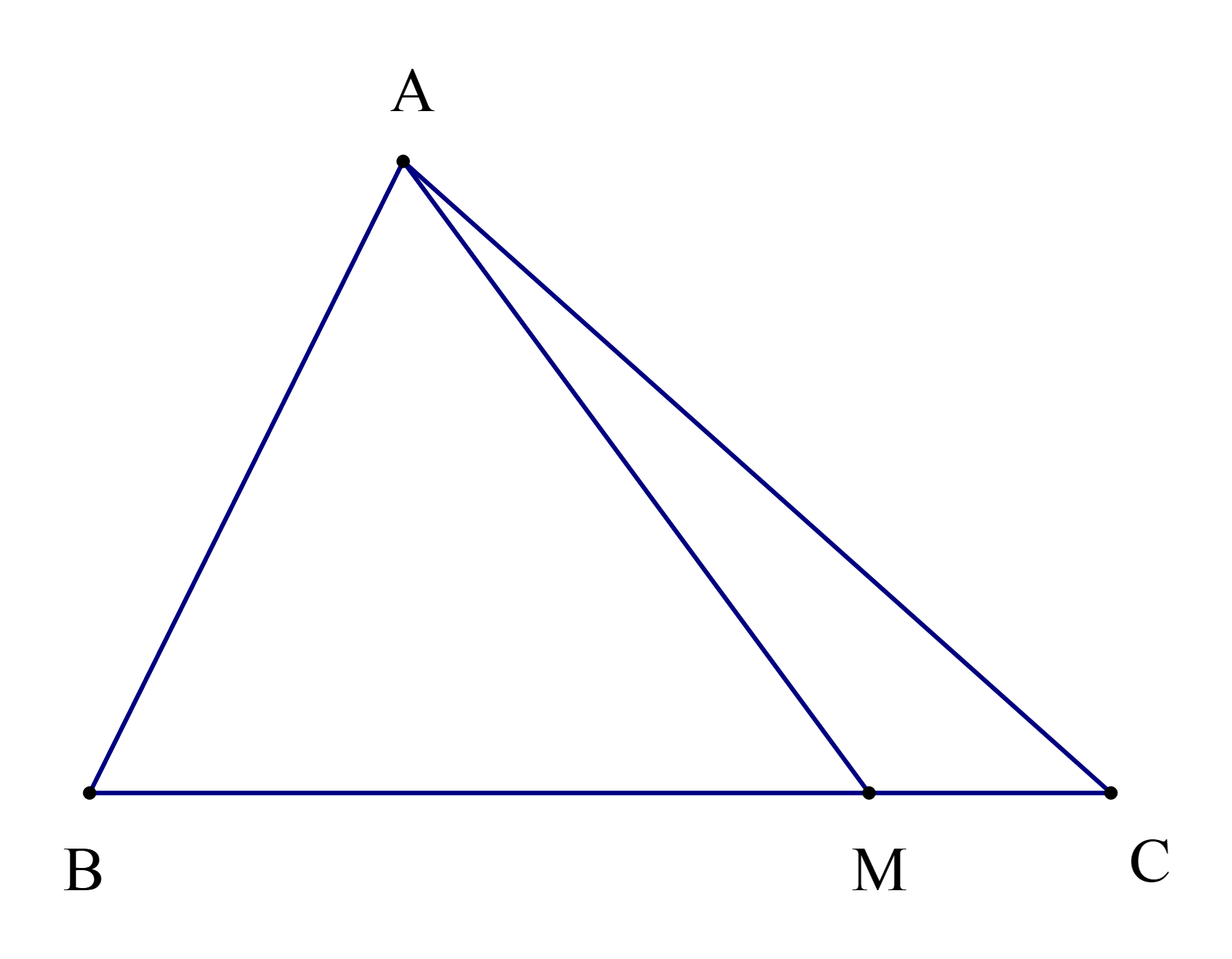
Chọn khẳng định đúng:
Hướng dẫn giải
Đáp án đúng là: A
Theo bài ta có: \(\widehat {{\rm{AMC}}} - \widehat {{\rm{AMB}}} = 80^\circ \)
Suy ra \(\widehat {{\rm{AMC}}} = 80^\circ + \widehat {{\rm{AMB}}}\) (1)
Ta lại có \(\widehat {{\rm{AMB}}}\) và \(\)\(\widehat {{\rm{AMC}}}\) là hai góc kề bù nên:
\(\widehat {{\rm{AMB}}}{\rm{ + }}\widehat {{\rm{AMC}}} = 180^\circ \) (2)
Thay (1) vào (2) ta có:
\(\widehat {{\rm{AMB}}}{\rm{ + 80}}^\circ {\rm{ + }}\widehat {{\rm{AMB}}} = 180^\circ \)
Suy ra \(2\widehat {{\rm{AMB}}} = 180^\circ - 80^\circ = 100^\circ \)
Suy ra \(\widehat {{\rm{AMB}}} = \frac{{100^\circ }}{2} = 50^\circ \)
Thay \(\widehat {{\rm{AMB}}} = 50^\circ \) vào (1) ta có:
\(\widehat {{\rm{AMC}}} = 80^\circ + 50^\circ = 130^\circ \)
Vậy \(\widehat {{\rm{AMB}}} = 50^\circ \);\(\widehat {{\rm{AMC}}} = 130^\circ \).
Câu 3:
Cho hình vẽ.
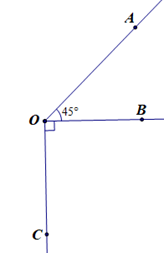
Kẻ tia OE là tia đối của tia OB và tia OD nằm giữa hai tia OC và OE sao cho \(\widehat {{\rm{COD}}} = \widehat {{\rm{DOE}}}.\) Chọn khẳng định sai:
Hướng dẫn giải
Đáp án đúng là: C
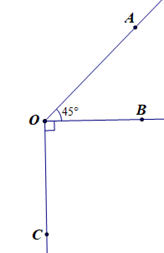
Theo bài ta có: CO ⊥ OB mà OE là tia đối của OB.
Do đó CO ⊥ EB
Suy ra \(\widehat {{\rm{COE}}} = 90^\circ \)
Theo bài \(\widehat {{\rm{COD}}} = \widehat {{\rm{DOE}}}\) và \(\widehat {{\rm{COD}}} + \widehat {{\rm{DOE}}} = \widehat {{\rm{COE}}}\) (hai góc kề nhau)
Suy ra \(\widehat {{\rm{COD}}} = \widehat {{\rm{DOE}}} = \frac{{90^\circ }}{2} = 45^\circ .\)
Ta có \(\widehat {{\rm{AOB}}} + \left( {\widehat {{\rm{BOC}}} + \widehat {{\rm{COD}}}} \right) = 45^\circ + 90^\circ + 45^\circ = 180^\circ .\)
Hay \(\widehat {{\rm{AOB}}} + \widehat {{\rm{BOD}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{AOB}}}\) và \(\widehat {{\rm{BOD}}}\) là hai góc bù nhau (vì hai góc bù nhau có tổng số đo bằng 180°) nên A đúng.
• Ta lại có \(\widehat {{\rm{AOB}}}\) và \(\widehat {{\rm{BOD}}}\) có chung cạnh OB và không có điểm trong chung nên hai góc \(\widehat {{\rm{AOB}}}\) và \(\widehat {{\rm{BOD}}}\) là hai góc kề nhau.
Vì hai góc \(\widehat {{\rm{AOB}}}\) và \(\widehat {{\rm{BOD}}}\) vừa kề nhau và vừa bù nhau nên \(\widehat {{\rm{AOB}}}\) và \(\widehat {{\rm{BOD}}}\) là hai góc kề bù. Do đó B đúng.
• Ta có \(\widehat {{\rm{AOB}}} + \widehat {{\rm{BOD}}} = 180^\circ \)(chứng minh trên)
Hay \(\widehat {{\rm{AOD}}} = 180^\circ \) suy ra OA và OD là hai tia đối nhau.
Mà OB và OE là hai tia đối nhau (giả thiết).
Do đó hai góc \(\widehat {{\rm{AOB}}}\) và \(\widehat {{\rm{EOD}}}\) là hai góc đối đỉnh nên D đúng.
• Ta có \(\widehat {{\rm{AOB}}} = \widehat {{\rm{COD}}} = 45^\circ \);
OA và OD là hai tia đối nhau nhưng OB và OC không phải là hai tia đối nhau.
Do đó \(\widehat {{\rm{AOB}}}\) và \(\widehat {{\rm{COD}}}\) không là hai góc đối đỉnh nên C sai.
Vậy ta chọn phương án C.
