Để chứng minh định lí: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”, ta có thể sử dụng khẳng định nào sau đây:
Giải bởi qa.haylamdo.com
Hướng dẫn giải:
Đáp án đúng là: B
Định lí: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra từ: “Nếu hai đường thẳng phân biệt cùng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì chúng song song với nhau”.
Thật vậy ta có thể chứng minh định lí như sau:
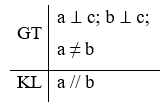
Chứng minh (hình vẽ dưới đây):
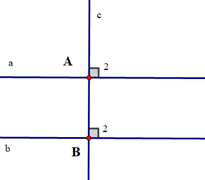
Ta có a ⊥ c (giả thiết) suy ra \({\widehat A_2} = {90^o}\);
b ⊥ c (giả thiết) suy ra \({\widehat B_2} = {90^o}.\)
Do đó \({\widehat A_2} = {\widehat B_2}\left( { = 90^\circ } \right)\)
Mà \({\widehat A_2}\) và \({\widehat B_2}\) là hai góc ở vị trí đồng vị.
Suy ra a // b.
Vậy ta chọn phương án B.
Cho hình vẽ minh họa cho giả thiết: aa' cắt cc’ tại A; bb' cắt cc’ tại B; aa’ // bb’.
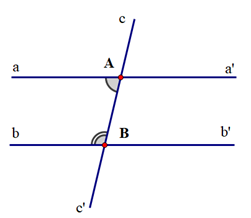
Cho các kết luận sau:
(I) \[\widehat {ABb} + \widehat {aAB} = 180^\circ ;\]
(II) \[\widehat {aAB} = \widehat {ABb'};\]
(III) \[\widehat {a'AB} + \widehat {ABb'} = 180^\circ .\]
Có bao nhiêu kết luận là đúng?
Cho giả thiết “Hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau, được minh họa như hình vẽ dưới đây:
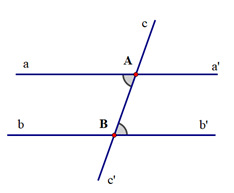
Kết luận nào sau đây là sai:
