Qua điểm A ở ngoài đường thẳng a vẽ 101 đường thẳng. Chứng tỏ rằng ít nhất cũng có 100 đường thẳng cắt a.
Giải bởi qa.haylamdo.com
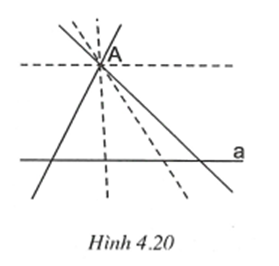
Giả sử trong số 101 đường thẳng vẽ qua A có chưa đến 100 đường thẳng cắt a. Suy ra ít nhất cũng còn hai đường thẳng không cắt a. Hai đường thẳng này cùng đi qua A và cùng song song với a. Điều này vô lí vì nó trái với tiên đề Ơ-clít. Vậy điều giả sử là sai, do đó qua A có ít nhất 100 đường thẳng cắt a.
Cho tam giác ABC, ; . Trên nửa mặt phẳng bờ BC có chứa A vẽ các tia Cx và Cy sao cho ACx=75; BCy=120. Chứng tỏ rằng các tia Cx và Cy trùng nhau.
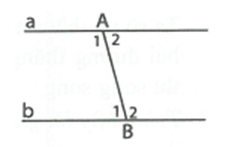
Cho tam giác ABC. Từ điểm M trên cạnh BC vẽ MD//AB, ME//AC. Xác định vị trí của điểm M để tia MA là tia phân giác của góc DME.
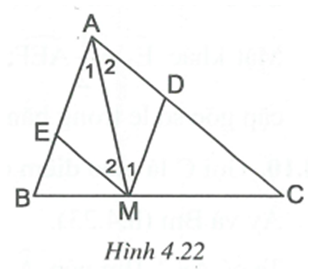
Cho tam giác ABC. Vẽ điểm M sao cho góc BAM bằng và so le trong với góc B. Vẽ điểm N sao góc CAN bằng và so le trong với góc C. Chứng tỏ rằng ba điểm M, A, N thẳng hàng.
Hình 4.11 có ABAC, CD và OE . Biết ; . Tìm giá trị m để tia OE là tia phân giác của góc AOC.
Cho điểm O ở ngoài đường thẳng xy. Qua O vẽ n đường thẳng. Xác định giá trị nhỏ nhất của n để trong số các đường thẳng đã vẽ, ít nhất cũng có 10 đường thẳng cắt xy.
Cho góc AOB. Trên tia OA lấy điểm M, trên tia OB lấy điểm N. Vẽ ra ngoài góc AOB các tia Mx và Ny song song với nhau. Cho biết , . tính số đo của góc AOB.
