Tập nghiệm của phương trình là
A.
B.
C.
D.
Giải bởi qa.haylamdo.com
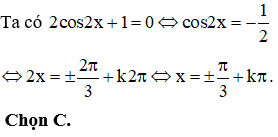
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất trong 5 tấm được chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4 là
Cho x, y là các số dương . Giá trị nhỏ nhất của là . Tích ab bằng
Người ta viết thêm 999 số thực vào giữa số 1 và số 2018 để được một cấp số cộng có 1001 số hạng. Tính số hạng thứ 501.
Cho a, b là hai số thực sao cho hàm số liên tục trên R. Tính a - b.
Cho hàm số y = f(x) xác định, liên tục trên R và có đạo hàm f'(x). Biết rằng hàm số f'(x) có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng?
Cho phương trình , m là tham số thực. Có bao nhiêu giá trị nguyên của để phương trình có nghiệm?
Thầy Hùng vay ngân hàng 100 triệu đồng, với lãi suất 1,1% /tháng. Thầy muốn hoàn nợ cho ngân hàng theo cách: sau đúng một tháng kể từ ngày vay, anh bắt đầu hoàn nợ, và những lần tiếp theo cách nhau đúng một tháng. Số tiền hoàn nợ ở mỗi lần là như nhau và trả hết nợ sau đúng 18 tháng kể từ ngày vay. Hỏi theo cách đó, số tiền lãi mà thầy Hùng ĐZ phải trả là bao nhiêu (làm tròn đến kết quả hàng nghìn)? Biết rằng, lãi suất ngân hàng không thay đổi trong suốt thời gian mà thầy vay.
Tìm điểm M thuộc sao cho qua M kẻ được duy nhất một tiếp tuyến tới (C).
Cho hàm số . Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số có cực tiểu mà không có cực đại. Tính tổng các phần tử của tập S.
Cho a, x là các số thực dương và thỏa mãn . Tìm giá trị lớn nhất của a?
Cho hàm số xác định, có đạo hàm trên đoạn [0;1] và thỏa mãn . Tính
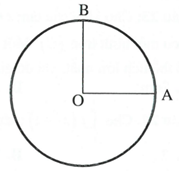
Cho hình tròn (C), bán kính R = 2. Cắt hình tròn (C) (như hình vẽ), rồi lấy hình tròn đó dán kín OA và OB lại để tạo ra mặt xung quanh của một hình nón. Tính diện tích toàn phần của hình nón.
Parabol chia hai đường tròn có tâm tại gốc tọa độ, bán kính bằng thành 2 phần. Tỉ số diện tích của chúng thuộc khoảng nào trong các khoảng sau đây?
Với các số dương a,b bất kì, đặt . Mệnh đề nào dưới đây là đúng?
