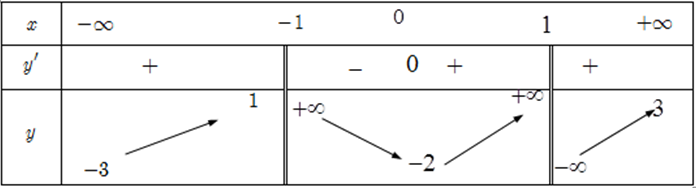
Cho hàm số y = f(x). Hàm số y = f’(x) có đồ thị như hình bên. Hàm số y = f(x2) có bao nhiêu điểm cực trị?
A. 3
B. 1
C. 5
D. 2
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Tìm giá trị lớn nhất M của hàm số y = x3 – 3x2 trên đoạn [-1; 1].
Khối hộp chữ nhật ABCD.A’B’C’D’ có độ dài AD, AD’, AC’ lần lượt là 1; 2; 3. Tính thể tích V của khối chóp A.A’B’C’D’.
Cho hàm số f(x) = |3x4 – 4x3 – 12x2 + m|. Gọi M là giá trị lớn nhất của hàm số trên đoạn [-1; 3] Giá trị nhỏ nhất của M bằng
Khối lăng trụ có diện tích đáy bằng 24 cm2, chiều cao bằng 3 cm thì có thể tích bằng
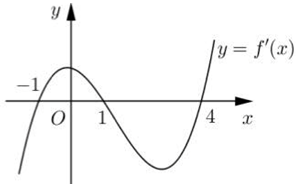
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Cho hàm số y = f(x) có đạo hàm liên tục trên R, thỏa mãn 2f(2x) + f(1 – 2x) = 12x2. Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ bằng 1 là
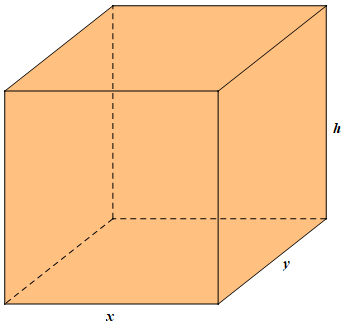
Một người thợ nhôm kính nhận đơn đặt hàng làm một bể cá cảnh bằng kính dạng hình hộp chữ nhật không có nắp có thể tích 3,2 m3; tỉ số giữa chiều cao của bể cá và chiều rộng của đáy bằng 2 (hình dưới). Biết giá một mét vuông kính để làm thành và đáy bể cá là 800 nghìn đồng. Hỏi người thợ đó cần tối thiểu bao nhiêu tiền để mua đủ số mét vuông kính làm bể cá theo yêu cầu (coi độ dày của kính là không đáng kể so với kích thước của bể cá).
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 1, mặt bên tạo với đáy góc 75o. Mặt phẳng (P) chứa đường thẳng AB và tạo với đáy góc 45o chia khối chóp S.ABCD thành hai khối đa diện. Thể tích của khối đa diện chứa đỉnh S bằng
Có bao nhiêu số nguyên dương m để hàm số nghịch biến trên khoảng (3; 6)?
Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB’D’.
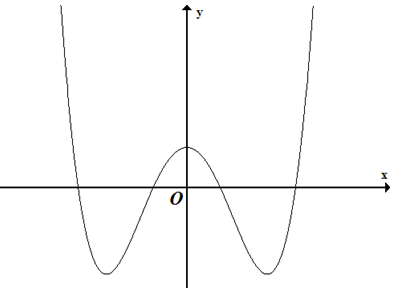
Cho hàm số y = f(x) có bảng biến thiên như sau
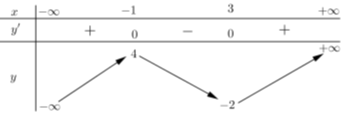
Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?
Cho hàm số y = f(x) xác định và có đạo hàm trên R \ { ± 1}. Hàm số có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận?