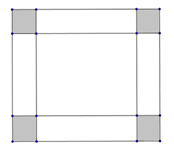
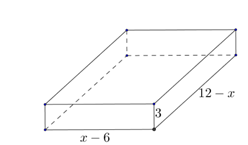
Một tấm kim loại hình chữ nhật có tổng chiều dài và chiều rộng là 18cm. Người ta cắt ở bốn gốc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng 3cm, rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Hỏi chiều rộng ban đầu của hình chữ nhật bằng bao nhiêu để hộp nhận được có thể tích lớn nhất ?
A. 7,5 cm
B. 9 cm
C. 6 cm
D. 3 cm
Giải bởi qa.haylamdo.com
Đáp án B
Gọi chiều rộng của hình chữ nhật ban đầu là x (cm), 0 < x < 18
=> Chiều dài của hình chữ nhật ban đầu là 18 - x(cm)
Hình hộp tạo thành có chiều dài là 18 - x - 6 = 12 - x(cm), chiều rộng là x - 6 (cm) và chiều cao là (3cm). Do thể tích của hình hộp là
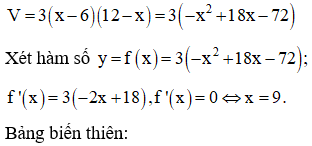
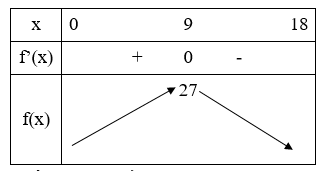
Từ bảng biến thiên suy ra thể tích lớn nhất 
Ông Minh vay ngân hàng 300 triệu đồng để xây nhà theo phương thức trả góp với lãi suất 0,5% mỗi tháng. Nếu đầu mỗi tháng, bắt đầu từ tháng thứ nhất ông hoàn nợ cho ngân hàng 6.000.000 đồng và chịu lãi số tiền chưa trả. Hỏi số tháng tối thiểu để ông Minh có thể trả hết số tiền đã vay là bao nhiêu ?
Cho hình chóp S.ABCD có đáy là hình chữ nhật, các mặt và vuông góc với đáy. Góc giữa (SCD) và mặt đáy bằng , BC = a, Tính khoảng cách giữa AB và SC theo a.
Cho mặt phẳng và điểm . Tọa độ của điểm M' đối xứng với M qua mặt phẳng (P) là
Cho số phức z thỏa mãn điều kiện là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
Cho tam giác vuông ABC với cạnh huyền . Mặt cầu đi qua ba điểm A, B, C có bán kính bé nhất bằng
Cho một khối chóp có thể tích bằng V. Khi giảm chiều cao của hình chóp xuống 2 lần và tăng diện tích đáy lên 4 lần thì thể tích khối chóp lúc đó bằng
Trong hệ trục tọa độ Oxyz, cho d là giao tuyến của hai mặt phẳng và . Mặt phẳng (P) đi qua d và vuông góc với mặt phẳng (Oyz) có phương trình là
Trong không gian tọa độ Oxyz, cho hai điểm và . Tọa độ điểm M nằm trên trục Oz và cách đều hai điểm A, B là
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau, . Tính thể tích của khối chóp S.ABC.
Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu (bỏ qua sức cản của không khí). Độ cao cực đại của viên đạn là bao nhiêu mét ? (cho gia tốc trọng trường )
Cho hàm số . Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Khi đó bằng
Cho tam giác ABC có . Phép tịnh tiến biến tam giác ABC thành tam giác A’B’C’. Tọa độ trọng tâm tam giác A’B’C’ là
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, . Kẻ . Mặt phẳng (AHK) cắt SC tại I. Tính thể tích khối cầu ngoại tiếp khối ABCDIHK.
