Cho hình chóp S.ABC có đáy là tam giác vuông cận tại B, . Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng . Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu .
A.
B.
C.
D.
Giải bởi qa.haylamdo.com
Đáp án C
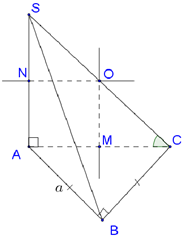
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM//SA
=> OM là trục của đường tròn ngoại tiếp tam giác ABC,
=> OA = OB = OC
Mặt khác, tam giác SAC vuông tại A, do đó OA = OS = OC
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ABC có thể tích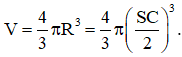 
A là hình chiếu của S lên mặt phẳng (ABC), do đó góc 
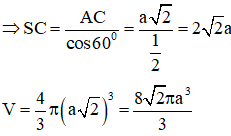
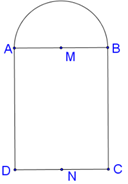
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết . Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
Diện tích hình phẳng được giới hạn bởi đường cong và đường thẳng , trục hoành trong miền bằng
Cho hình lăng trụ đứng tam giác , tam giác ABC có , góc , . Tính thể tích khối lăng trụ là
Trong không gian cho đường thẳng d có phương trình . Một véctơ chỉ phương của d là
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3) và đường thẳng . Xác định tọa độ điểm M' là điểm đối xứng với M qua đường thẳng d.
Tìm m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác có diện tích bằng 4.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu và mặt phẳng . Khẳng định nào sau đây là đúng?
