Trong mặt phẳng Oxy, cho điểm A(2;2) và các đường thẳng . Biết rằng tồn tại điểm thuộc đường thẳng và điểm thuộc đường thẳng sao cho tam giác ABC vuông cân tại A. Tính giá trị của biểu thức , biết điểm B có hoành độ không âm.
A. T = -14
B. T = 18
C. T = 11
D. T = 14
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn đáp án D.

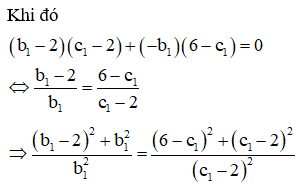

Cách 2: Vì tam giác ABC vuông cân tại A nên phép quay tâm A với góc quay
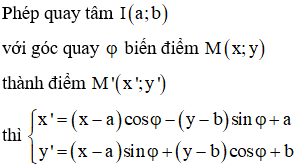
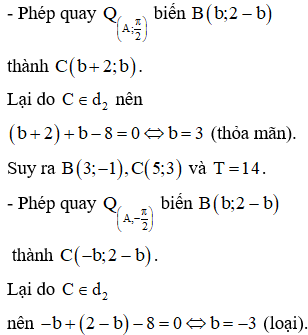
Trong không gian Oxyz, cho đường thẳng . Gọi Δ là đường thẳng đi qua điểm và có vectơ chỉ phương . Đường phân giác của góc nhọn tạo bởi d và Δ có phương trình là
Cho các số dương a, b, c thỏa mãn . Khi đó biểu thức có giá trị là
Cho tập hợp M gồm 15 điểm phân biệt. Số vectơ khác , có điểm đầu và điểm cuối là các điểm thuộc M là
Một người gửi tiết kiệm 200 triệu đồng vào một ngân hàng với lãi suất 6,8%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm số tiền lãi người đó thu được so với tiền gốc ban đầu có thể dùng để mua được một chiếc xe máy giá 47 990 000 đồng, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra?
Cho khối hộp . Gọi M là trung điểm của AB. Mặt phẳng chia khối hộp đã cho thành hai phần. Gọi là thể tích khối đa diện có chứa và là thể tích phần còn lại. Tính tỉ số .
Biết rằng tồn tại các số nguyên a, b sao cho hàm số đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của bằng
Trong không gian Oxyz, cho các điểm . Biết rằng tồn tại duy nhất điểm khác gốc tọa độ để SA, SB, SC đôi một vuông góc. Tính tổng bình phương giá trị của a, b và c.
Trong một cuộc khảo sát, 607 bác sĩ phẫu thuật chỉnh hình và tổng quát về các hoạt động chuyên môn chính của họ. Kết quả được cho bởi bảng sau:
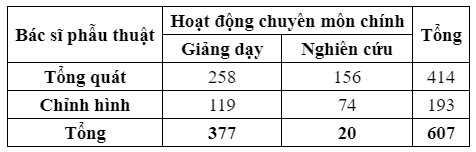
Chọn ngẫu nhiên một bác sĩ phẫu thuật, số nào dưới đây gần với xác suất để bác sĩ được chọn là một bác sĩ tổng quát có hoạt động chuyên môn chính là giảng dạy?
Khẳng định nào dưới đây là sai về tâm của mặt cầu ngoại tiếp hình hộp chữ nhật ?
Cho 10 cái thẻ, mỗi thẻ được viết một số nguyên dương thuộc đoạn sao cho hai thẻ khác nhau được viết hai số khác nhau. Chọn ngẫu nhiên 3 thẻ và tính tích của ba số được ghi trên 3 thẻ. Tính xác suất để tích của ba số trên 3 thẻ được chọn là một số chia hết cho 3.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và điểm . Viết phương trình mặt phẳng , biết rằng điểm B thuộc mặt cầu , có hoành độ dương và tam giác OAB đều.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và . Chọn hệ trục tọa độ Oxyz sao cho A trung với O, điểm B thuộc tia Ox, điểm D thuộc tia Oy và điểm S thuộc tia Oz. Gọi G là trọng tâm của tam giác SBD. Mệnh đề nào dưới đây là đúng?
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và và . Thể tích của khối chóp S.ABC bằng
Cho hai số phức thỏa mãn điều kiện và . Biết rằng , trong đó m, n, p là các số nguyên dương và phân số tối giản. Tính .