Cho một đa giác đều có 48 đỉnh. Lấy ngẫu nhiên ba đỉnh của đa giác. Tính xác suất để tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn.
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
Xác suất của biến cố A được tính bởi công thức:
Cách giải:
Số cách chọn 3 đỉnh bất kì của đa giác là:
Gọi O là tâm đường tròn ngoại tiếp đa giác đều.
Gọi biến cố A: “Chọn 3 đỉnh bất kì của đa giác để được một tam giác nhọn”.
Lấy điểm A thuộc đường tròn (O), kẻ đường kính AA’ => A’ cũng thuộc đường tròn (O).
Khi đó AA’ chia đường tròn (O) thành hai nửa, mỗi nửa có 23 đỉnh.
Chọn 2 đỉnh B, C cùng thuộc 1 nửa đường tròn có có tam giác ABC là tam giác tù.
Tương tự như vậy đối với nửa còn lại nên ta có 2 tam giác tù được tạo thành.
Đa giác đều có 48 đỉnh nên có 24 đường chéo => có 24.2. tam giác tù.
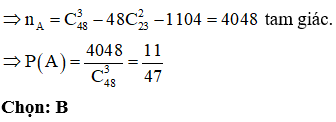
Ứng với mỗi đường kính ta có 23.2 tam giác vuông. Vậy số tam giác vuông là: 23.2.24 = 1104 tam giác.
Cho khối chóp tứ giác SABCD có thể tích V, đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm các cạnh SB, BC, CD, DA. Tính thể tích khối chóp M.CNQP theo V.
Cho hai số thực a > 1, b > 1. Gọi là hai nghiệm của phương trình . Trong trường hợp biểu thức đạt giá trị nhỏ nhất, mệnh đề nào sau đây là đúng?
Cho hàm số . Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và các đường thẳng
Cho hình chóp tam giác S.ABC có đáy ABC là một tam giác vuông cân tại B với trọng tâm G, cạnh bên SA tạo với đáy (ABC) một góc . Biết hai mặt phẳng cùng vuông góc với mặt phẳng (ABC). Tính cosin của góc giữa hai đường thẳng SA và BC.
Tính diện tích hình phẳng giới hạn bởi các điểm biểu diễn các số phức thỏa mãn
Cho hình lập phương cạnh a. Tính diện tích toàn phần của vật tròn xoay thu được khi quay tam giác quanh trục AA'
Cho hai dãy ghế dối diện nhau, mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam, 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ.
Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là một tam giác đều và nằm trong một mặt phẳng vuông góc với đáy (ABCD). Tính thể tích khối chóp SABCD.
Cho hàm số có đồ thị (C). Gọi A, B, C, D là bốn điểm trên đồ thị (C) với hoành độ lần lượt là a, b, c, d sao cho tứ giác ABCD là một hình thoi đồng thời hai tiếp tuyến tại A, C song song với nhau và đường thẳng AC tạo với hai trục tọa độ một tam giác cân. Tính tích abcd.