Một tam giác có chu vi bằng 36cm, ba cạnh của tam giác đó lần lượt tỉ lệ thuận với 3; 4; 5. Tính độ dài ba cạnh của tam giác đó.

Nếu góc xOy có số đo bằng 47^o thì số đo của góc đối đỉnh với góc xOy bằng bao nhiêu?

Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.

a) Chứng minh: ∆OAD = ∆OCB.

b) Chứng minh: IA = IC.

c) Chứng minh: OI là tia phân giác của $\widehat{xOy}$.

Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.

a) Chứng minh: ∆OAD = ∆OCB.

b) Chứng minh: IA = IC.

c) Chứng minh: OI là tia phân giác của $\widehat{xOy}$.

Tìm x, y biết: $\frac{1+3y}{12}=\frac{1+5y}{5x}=\frac{1+7y}{4x}$.

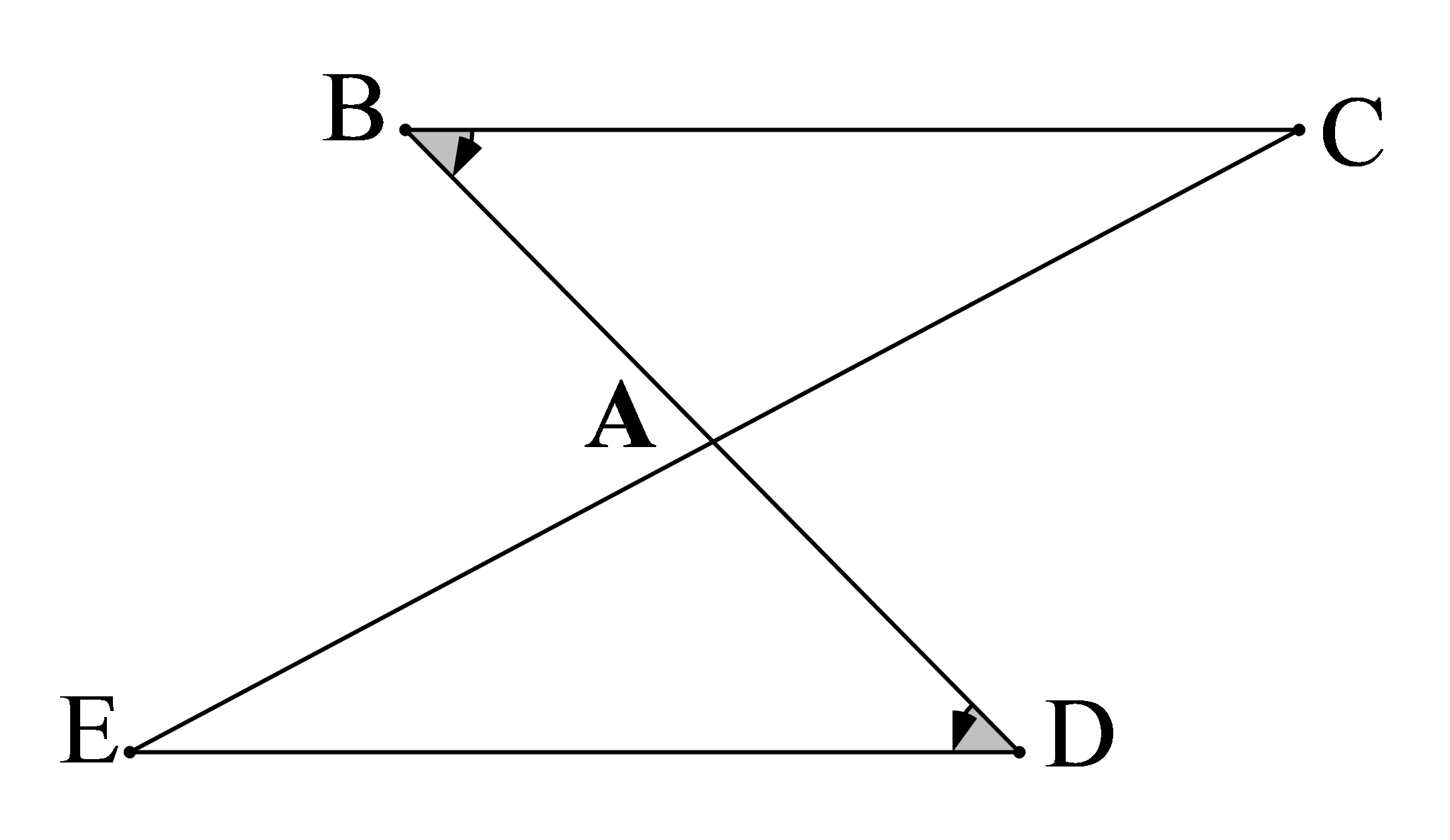
Với các kí hiệu trên hình vẽ, cần có thêm yếu tố nào nữa để kết luận ∆ABC = ∆ADE (g.c.g) ?

Kết quả phép tính $\frac{-3}{8}+\frac{5}{6}$ là:

Cho hình vẽ sau:

Tọa độ điểm M là:

Thực hiện phép tính (tính bằng cách hợp lý nếu có thể)

a) $-1\frac{1}{2}.21\frac{1}{3}+1\frac{1}{2}.1\frac{1}{3}$

b) $\frac{{(-2)}^3}{5}.|\frac{1}{4}-1|+{2018}^0$.

Trong các phân số sau, phân số nào biểu diễn số hữu tỉ $-\frac{3}{4}$?

Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 15. Hệ số tỉ lệ k của y đối với x là:

Tìm x, biết:

a) $(\mathrm{0,5}x-\frac{3}{7}):\frac{1}{2}=1\frac{1}{7}$

b) |2 − 3x| − 5 = −1

c) ${(\frac{1}{5}-\frac{3}{2}x)}^2=\frac{9}{4}$.

Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.

a) Chứng minh: ∆OAD = ∆OCB.

b) Chứng minh: IA = IC.

c) Chứng minh: OI là tia phân giác của $\widehat{xOy}$.