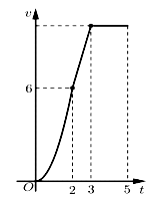
Một chiếc xe đua đạt tới vận tốc lớn nhất là 360 km/h. Đồ thị bên biểu thị vận tốc v của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu là một phần của một parabol định tại gốc tọa độ O, giây tiếp theo là đoạn thẳng và sau đúng ba giây thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trực tung biểu thị 10 m/s và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó xe đã đi được quãng đường là bao nhiêu?
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
- Tìm hàm vận tốc v(t) trên mỗi giai đoạn dựa vào đồ thị.
- Quãng đường vật đi được từ thời điểm t = a đến thời điểm t = b là
Cách giải:
Trong 2 giây đầu, lại có khi nên suy ra
Quãng đường vật đi được trong 2 giây đầu là
Trong giây tiếp theo,
Ta có nên ta có hệ phương trình
Quãng đường vật đi được trong giây tiếp theo là
Trong 2 giây cuối,
Quãng đường vật đi được trong 2 giây cuối là
Vậy trong 5 giây đó xe đã đi được quãng đường là:
Chọn D.
Một tổ học sinh có 12 bạn, gồm 7 nam và 5 nữ. Cần chọn một nhóm 3 học sinh của tổ đó để làm vệ sinh lớp học. Hỏi có bao nhiêu cách chọn sao cho trong nhóm có cả nam và nữ?
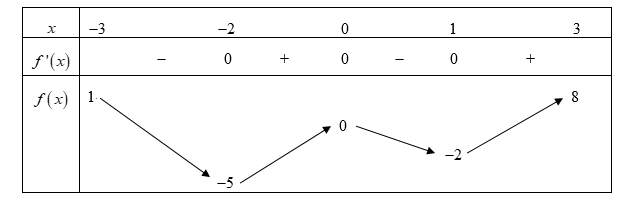
Cho hàm số y = f(x) có bảng biến thiên như hình bên. Giá trị lớn nhất của hàm số đã cho trên đoạn [-3; 3] bằng:
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân, AB = BC = 2a. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
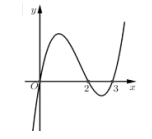
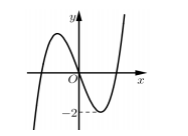
Cho hàm số bậc ba y = f(x) có đồ thị như hình bên. Phương trình có bao nhiêu nghiệm?
Có bao nhiêu số phức z đôi một khác nhau thỏa mãn và là số thực?
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, O là tâm của mặt đáy. Khoảng cách giữa hai đường thẳng SO và CD bằng
Có bao nhiêu số nguyên a để phương trình có hai nghiệm thực phân biệt.