Tập nghiệm của bất phương trình log4(x+7)>log2(x+1) là khoảng (a; b). Giá trị M=2a−b bằng
Giải bởi qa.haylamdo.com
Phương pháp:
- Tìm ĐKXĐ.
- Đưa về cùng cơ số.
- Giải bất phương trình logarit: logax>logay⇔x>y(a>1).
Cách giải:
ĐKXĐ: {x+7>0x+1>0⇔{x>−7x>−1⇔x>−1.
Ta có
log4(x+7)>log2(x+1)
⇔log4(x+7)>log4(x+1)2
⇔x+7>(x+1)2
⇔x2+x−6<0
⇔−3<x<2
Kết hợp ĐKXĐ ta có -1 < x < 2
⇒ Tập nghiệm của bất phương trình là S=(−1;2)⇒{a=−1b=2.
Vậy M=2a−b=2(−1)−2=−4.
Chọn D.
Cho I=e∫1lnxx(lnx+2)2dx=aln3+bln2+c3 với a,b,c∈ℤ. Giá trị a2+b2+c2 bằng
Từ các số 1, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau.
Cho hàm số f(x)=2x−mx+2 (m là tham số). Để minx∈[−1;1]f(x)=13 thì m=ab(a∈ℤ,b∈ℕ,b>0). Tổng a + b bằng
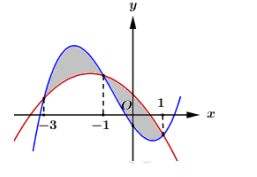
Cho hai hàm số f(x)=ax3+bx2+cx−12 và g(x)=dx2+ex+1(a,b,c,d,e∈ℝ), biết rằng đồ thị hàm số y = f(x) và y = g(x) cắt nhau tại 3 điểm có hoành độ lần lượt là -3; -1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng
Cho hàm số y = f(x) có bảng biến thiên như sau:
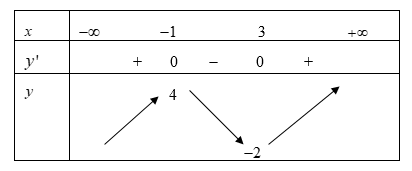
Giá trị cực đại của hàm số đã cho là
