Cho hàm số f(x)=25m2x5−83mx3−(m2−m−20)x+1. Có bao nhiêu giá trị nguyên của tham số m để hàm số đã cho đồng biến trên ℝ?
Giải bởi qa.haylamdo.com
Phương pháp:
- Tính f'(x)
- Hàm số đã cho đồng biến trên ℝ khi f' và bằng 0 tại hữu hạn điểm.
- Đặt Đưa (*) về dạng
Cách giải:
Ta có
Hàm số đã cho đồng biến trên khi và bằng 0 tại hữu hạn điểm.
Đặt Khi đó
Vậy có 8 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn C.
Từ các số 1, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau.
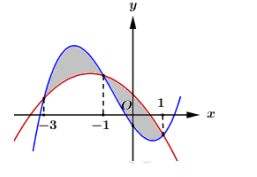
Cho hai hàm số và biết rằng đồ thị hàm số y = f(x) và y = g(x) cắt nhau tại 3 điểm có hoành độ lần lượt là -3; -1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng
Cho hàm số y = f(x) có bảng biến thiên như sau:
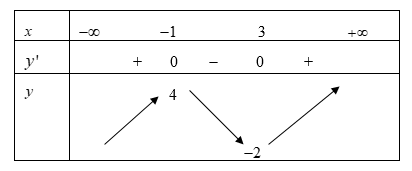
Giá trị cực đại của hàm số đã cho là
