Cho số phức thỏa mãn và môđun của số phức đạt giá trị nhỏ nhất. Khi đó giá trị bằng
C. 1
Giải bởi qa.haylamdo.com
Phương pháp:
- Thay z = a + bi vào biểu thức từ đó tìm mối liên hệ giữa a, b và tìm điều kiện của b
- Tính theo b
- Sử dụng phương pháp hàm số để tìm GTNN của biểu thức.
Cách giải:
Ta có:
Khi đó:
Do nên
Ta có
Xét hàm số với ta có
Hàm số y = f(x) là hàm số đồng biến trên do đó
Khi đó
Vậy khi môđun của số phức đạt giá trị nhỏ nhất thì
Chọn D.
Từ các số 1, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau.
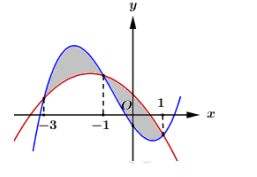
Cho hai hàm số và biết rằng đồ thị hàm số y = f(x) và y = g(x) cắt nhau tại 3 điểm có hoành độ lần lượt là -3; -1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng
Cho hàm số y = f(x) có bảng biến thiên như sau:
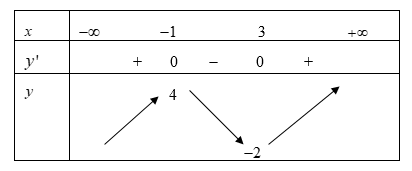
Giá trị cực đại của hàm số đã cho là
