Xét tất cả các số thực dương a và b thỏa mãn Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
- Đưa về cùng cơ số, sử dụng công thức
- Sử dụng công thức .
Cách giải:
Chọn D.
Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tích là một số lẻ bằng:
Có bao nhiêu số nguyên a thuộc đoạn [-20; 20] sao cho hàm số có cực đại?
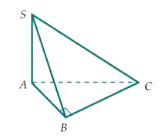
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác vuông tại và BC = a (minh họa hình vẽ bên dưới). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ sau:
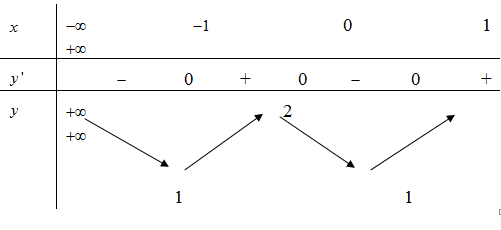
Số nghiệm thực của phương trình là:
Cho các số thực dương a, b khác 1 thỏa mãn và ab = 64. Giá trị của biểu thức bằng:
Trong không gian Oxyz, phương trình mặt cầu (S) có tâm I(-1; 2; 1) và đi qua điểm A(0; 4; -1) là:
Cho hàm số y = f(x) có đồ thị như hình vẽ sau:
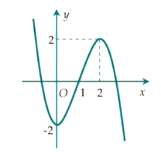
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?