A. (6; 7)
B. (7; 8)
C. (9; 10)
D. (8; 9)
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
Giả sử vật thể T giới hạn bởi hai mặt phẳng x = a, x = b. Cắt vật thể T bởi một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ được thiết diện có thể tích S(x) Khi đó thể tích vật thể T là
Cách giải:
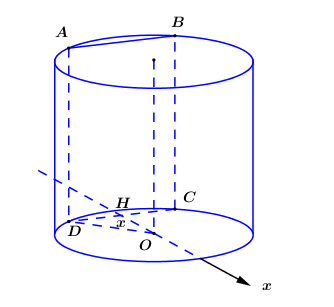
Giả sử vật thể là hình trụ Thiết diện ABCD là hình vuông.
Ta có
Khi đó thể tích vật thể là:
Chọn B.
Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc S xác suất để số đó có hai chữ số tận cùng không có cùng tính chẵn lẻ bằng:
Cho hàm số f(x) liên tục trên và có bảng xét dấu của f'(x) như sau:

Số điểm cực tiểu của hàm số đã cho là:
Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh 2a. Cạnh bên SA vuông góc với mặt phẳng đáy, SA = 2a. Tính thể tích V của khối chóp S.ABCD.
Cho hình lăng trụ đứng ABC.A'B'C' có Gọi D là trung điểm của CC' và Tính thể tích V của khối lăng trụ ABC.A'B'C'.
Cho tam giác đều ABC có cạnh bằng 4. Gọi H là trung điểm cạnh BC. Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AH là:
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình vẽ dưới
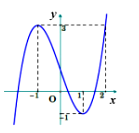
Số nghiệm thực của phương trình là:
Cho hàm số y = f(x) có bảng biến thiên:
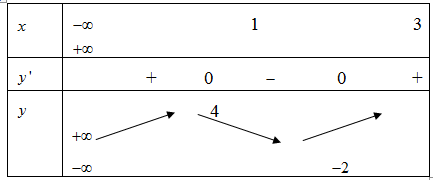
Có bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm phân biệt?
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình Phương trình mặt phẳng (P) tiếp xúc với mặt cầu tại điểm A(-1; -3; 4) là
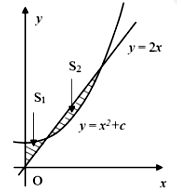
Cho đường thẳng y = 2x và parabol (c là tham số thực dương). Gọi và lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi thì c gần với số nào nhất sau đây?
Cho hàm số y = f(x) có bảng biến thiên như sau:
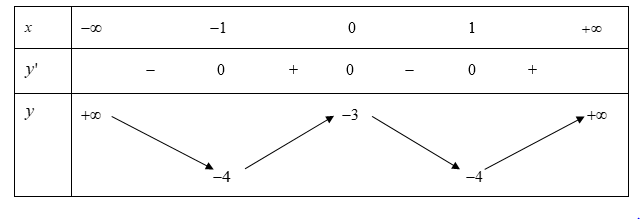
Giá trị cực đại của hàm số đã cho bằng
Trong không gian Oxyz, mặt cầu có tâm I(4; -4; 2) và đi qua gốc tọa độ có phương trình là: