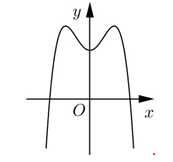
A. y=x4−2x2+2.
B. y=-x4+2x2+2.
C. y=x3−3x2+2.
D. y=-x3+3x2+2.
Giải bởi qa.haylamdo.com
Chọn B.
Đây là dạng đồ thị của hàm bậc 4 trùng phương có hệ số của x4 âm.
Trong không gian với hệ trục tọa độ Oxyz cho ba điểm A(1;0;0),B(0;2;0),C(0;0;3). Tâm mặt cầu ngoại tiếp tứ diện OABC có tọa độ I(a; b;c) tổng a + b + c bằng
Cho phương trình log3(3x2−6x+6)=3y2+y2−x2+2x−1. Hỏi có bao nhiêu cặp (x;y);0<x<2021;y∈ℕ thỏa mãn phương trình đã cho
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số f(x)=x|x|−1 là
Cho phương trình z2+az+b=0(a,b∈ℝ) có một nghiệm là 3 + 4i. Giá trị của biểu thức a + b bằng
Cho hàm số f(x) có bảng biến thiên như sau
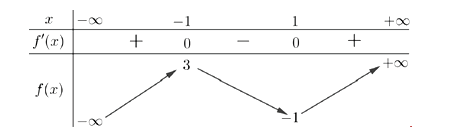
Số nghiệm của phương trình 3f(x) - 2 = 0 là
Cho phương trình log233x+log3x+m−1=0 (m là tam số thực). Số giá trị nguyên của m để phương trình đã cho có đúng 2 nghiệm phân biệt thuộc khoảng (0; 1)
