Khi kí hợp đồng lao động dài hạn với các kĩ sư được tuyển dụng, công ti liên doanh A đề xuất 2 phương án trả lương để người lao động tự lựa chọn, cụ thể:
+ Phương án 1: Người lao động nhận được 360 triệu đồng cho năm làm việc đầu tiên, và kể từ năm thứ 2 trở đi, mức lương sẽ tăng thêm 30 triệu đồng mỗi năm.
+ Phương án 2: Người lao động nhận được 70 triệu đồng cho quý làm việc đầu tiên, và kể từ quý thứ 2 trở đi, mức lương sẽ tăng thêm 5 triệu đồng mỗi quý.
Nếu em là người kí hợp đồng lao động em sẽ chọn phương án nào?
D. Không phương án nào
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Tính tổng lương trong 10 năm.
+ Theo phương án 1:
+ Theo phương án 2:
1 năm có 4 quý năm có 40 quý.
Vậy chọn phương án 2.
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{1}{3}{x^3} + 2m{x^2} + 8x - 2\) đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)?
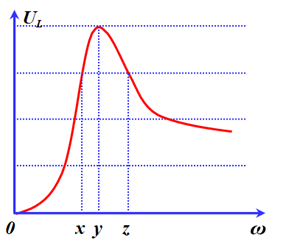
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi vào hai đầu đoạn mạch AB mắc nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C. Tần số góc ω của điện áp là thay đổi được. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên L theo giá trị tần số góc ω. Lần lượt cho ω bằng x, y và z thì mạch AB tiêu thụ công suất lần lượt là P1, P2 và P3. Biểu thức nào sau đây đúng?
Có 4 dung dịch: natri clorua (NaCl), rượu etylic (C2H5OH), axit axetic (CH3COOH), kali sunfat (K2SO4) đều có nồng độ 0,1 mol/lít. Dung dịch chứa chất tan có khả năng dẫn điện tốt nhất là
Chị Tâm gửi 340 triệu đồng vào ngân hàng với lãi suất 8,7%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Giả sử lãi suất không thay đổi và chị Tâm không rút tiền trong thời gian gởi tiền. Hỏi sau ít nhất bao nhiêu năm thì chị ấy có được số tiền nhiều hơn 680 triệu đồng (kể cả tiền vốn lẫn tiền lãi)?
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right)\) chứa trục \(Oz\) và đi qua điểm \(M\left( { - 1;1; - 1} \right)\) có phương trình là
Một nhóm học sinh có 8 học sinh nữ và 4 học sinh nam. Xếp ngẫu nhiên nhóm học sinh này thành một hàng dọc. Tính xác suất sao cho không có hai bạn nam nào đứng cạnh nhau.
Trong các hàm số sau, hàm số nào là một nguyên hàm của \(f\left( x \right) = \frac{1}{{1 - x}}\) trên khoảng \(\left( {1; + \infty } \right)\).
Đốt cháy hoàn toàn 6,46 gam hỗn hợp E gồm ba este no, mạch hở X, Y, Z (đều tạo bởi axit cacboxylic và ancol, MX < MY < MZ < 248) cần vừa đủ 0,235 mol O2, thu được 5,376 lít khí CO2. Cho 6,46 gam E tác dụng hết với dung dịch NaOH (lấy dư 20% so với lượng phản ứng) rồi chưng cất dung dịch, thu được hỗn hợp hai ancol đồng đẳng kế tiếp và hỗn hợp chất rắn khan T. Đốt cháy hoàn toàn T, thu được Na2CO3, CO2 và 0,18 gam H2O. Phân tử khối của Y là
Nếu hàm số \(f\left( x \right) = \sqrt {2x - 1} \) thì \(f'\left( 5 \right)\) bằng
Vì sao từ thập kỷ 60, 70 của thế kỷ XX, nhóm 5 nước sáng lập ASEAN thực hiện chiến lược kinh tế hướng ngoại?
Có 3 quả bóng tennis được chứa trong một hộp hình trụ (hình vẽ bên) với chiều cao 21cm và bán kính 3,5cm.

Thể tích bên trong hình trụ không bị chiếm bởi các quả bóng tennis (bỏ qua độ dày của vỏ hộp) bằng bao nhiêu?
Nhiệt phân hoàn toàn 23,15 gam hỗn hợp muối KNO3 và NH4NO3. Ngưng tụ toàn bộ hơi nước thu được hỗn hợp khí với tỉ lệ nN2O : nO2 = 4 : 3. Phần trăm khối lượng muối KNO3 trong hỗn hợp là
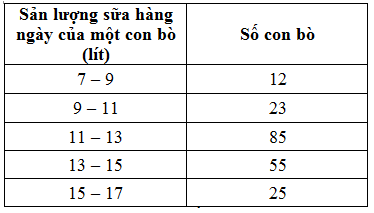
Trong một nông trường chăn nuôi bò sữa Ba Vì ta thu nhập được tài liệu sau:
Cho số phức \(z = a + bi{\mkern 1mu} {\mkern 1mu} \left( {a,{\mkern 1mu} {\mkern 1mu} b \in \mathbb{R}} \right)\) theo điều kiện \(\left( {2 - 3i} \right)z - 7i\bar z = 22 - 20i\). Tính \(S = a + b\).