Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x - y \le 2}\\{3x + 5y \le 15}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\). Khẳng định nào sau đây là khẳng định sai ?
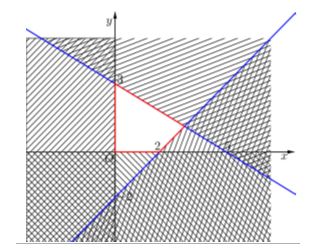
A.Trên mặt phẳng tọa độ Oxy, biểu diễn miền nghiệm của hệ bất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với \[A\left( {0;3} \right),B\left( {\frac{{25}}{8};\frac{9}{8}} \right),C\left( {2;0} \right)\] và O(0;0).
B.Đường thẳng \[\Delta :x + y = m\;\] luôn có giao điểm với miền nghiệm của hệ với mọi giá trị của m.
C.Giá trị lớn nhất của biểu thức x+y , với x và y thỏa mãn hệ bất phương trình đã cho là 174.
D.Giá trị nhỏ nhất của biểu thức x+y , với x và y thỏa mãn hệ bất phương trình đã cho là 0.
Giải bởi qa.haylamdo.com
Trước hết, ta vẽ bốn đường thẳng:
\[\left( {{d_1}} \right):x - y = 2\]
\[\left( {{d_2}} \right):3x + 5y = 15\]
\[\left( {{d_3}} \right):x = 0\]
\[\left( {{d_4}} \right):y = 0\]
- Miền nghiệm là phần không bị gạch, kể cả biên nên A đúng.
- Đáp án B sai vì nếu m = 5 ta vẽ đường thẳng x + y = 5 sẽ không có giao điểm với miền nghiệm của hệ.
- Ta sẽ tìm GTLN, GTNN của biểu thức\[F\left( {x;y} \right) = x + y\] với (x;y) là nghiệm của hệ.
Ta có:
\[\begin{array}{*{20}{l}}{F\left( {0;3} \right) = 0 + 3 = 3,F\left( {\frac{{25}}{8};\frac{9}{8}} \right) = \frac{{25}}{8} + \frac{9}{8} = \frac{{17}}{4},}\\{F\left( {2;0} \right) = 2 + 0 = 2,F\left( {0;0} \right) = 0 + 0 = 0}\end{array}\]
Đáp án cần chọn là: B
Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{{x^2} - 1 \le 0}\\{x - m >0}\end{array}} \right.\) có nghiệm khi và chỉ khi:
Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{m\left( {mx - 1} \right) < 2}\\{m\left( {mx - 2} \right) \ge 2m + 1}\end{array}} \right.\)có nghiệm khi và chỉ khi:
Biết rằng bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x - 1 < 2x - 3}\\{\frac{{5 - 3x}}{2} < x - 3}\\{3x \le x + 5}\end{array}} \right.\) có tập nghiệm là một đoạn \[[a;b].\]Hỏi a + b bằng:
Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{2x - \frac{3}{2}y \ge 1}\\{4x - 3y \le 2}\end{array}} \right.\)có tập nghiệm S. Khẳng định nào sau đây là khẳng định đúng?
Tập nghiệm S của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{2 - x >0}\\{2x + 1 < x - 2}\end{array}} \right.\) là:
Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{3x + 5 \ge x - 1}\\{{{(x + 2)}^2} \le {{(x - 1)}^2} + 9}\\{mx + 1 >(m - 2)x + m}\end{array}} \right.\) vô nghiệm khi và chỉ khi:
Tập nghiệm S của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{\frac{{2x - 1}}{3} >- x + 1}\\{\frac{{4 - 3x}}{2} < 3 - x}\end{array}} \right.\)là:
Tìm tất cả các giá trị thực của tham số mm để hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{2x - 1 \ge 3}\\{x - m \le 0}\end{array}} \right.\)có nghiệm duy nhất.
Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{{x^2} - 1 \le 0}\\{x - m >0}\end{array}} \right.\)có nghiệm khi
