Cho tứ diện ABCD có AB,BC,CD đôi một vuông góc với nhau. Điểm nào dưới đây cách đều bốn đỉnh A,B,C,D của tứ diện ABCD ?
A.Trung điểm của cạnh BD.
B.Tâm đường tròn ngoại tiếp tam giác ABC.
C.Trung điểm của cạnh AD.
D.Trọng tâm của tam giác ACD.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
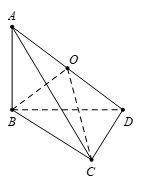
Ta có \(\left\{ {\begin{array}{*{20}{c}}{AB \bot BC}\\{AB \bot CD}\end{array}} \right. \Rightarrow AB \bot (BCD) \Rightarrow \) tam giác ABD vuông tại B.
Suy ra \[IA = IB = ID = \frac{{AD}}{2},\] với I là trung điểm của AD. (1)
Lại có \(\left\{ {\begin{array}{*{20}{c}}{AB \bot CD}\\{BC \bot CD}\end{array}} \right. \Rightarrow CD \bot (ABC) \Rightarrow \) tam giác ACD vuông tại C.
Suy ra \[EA = EC = ED = \frac{{AD}}{2},\] với E là trung điểm của AD. (2)
Từ (1),(2) suy ra \[I \equiv E \equiv O\] nên trung điểm của cạnh AD cách đều A,B,C,D.
Đáp án cần chọn là: C
Cho hình chóp S.ABCD có các cạnh bên bằng nhau SA=SB=SC=SD. Gọi H là hình chiếu của S lên mặt đáy ABCD. Khẳng định nào sau đây sai?
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại C. Cạnh bên SA vuông góc với đáy. Gọi H,K lần lượt là trung điểm của AB và SB. Khẳng định nào dưới đây sai ?
Cho hình chóp S.ABCD trong đó ABCD là hình chữ nhật, \[SA \bot (ABCD)\] Trong các tam giác sau tam giác nào không phải là tam giác vuông
Cho tứ diện ABCD có AB,BC,CD đôi một vuông góc với nhau và AB=a, BC=b,CD=c. Độ dài đoạn thẳng AD bằng
Trong không gian cho đường thẳng \[\Delta \] và điểm O. Qua O có mấy đường thẳng vuông góc với \[\Delta \] cho trước?
Cho hai đường thẳng phân biệt a,b và mặt phẳng(P), trong đó \[a \bot (P)\] Mệnh đề nào sau đây là sai?
Trong không gian tập hợp các điểm M cách đều hai điểm cố định A và B là
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA=SC, SB=SD. Khẳng định nào sau đây là đúng ?
Cho hình lập phương ABCD.A′B′C′D′. Đường thẳng AC′ vuông góc với mặt phẳng nào sau đây?
Cho hình chóp S.ABC có các mặt bên tạo với đáy một góc bằng nhau. Hình chiếu H của S trên (ABC) là
Trong không gian cho đường thẳng \[\Delta \] không nằm trong mp (P), đường thẳng \[\Delta \] được gọi là vuông góc với mp (P) nếu:
Cho hình chóp S.ABC có \[SA \bot (ABC)\;\] và tam giác ABC không vuông, gọi H,K lần lượt là trực tâm các tam giácABC và SBC. Các đường thẳng AH,SK,BC thỏa mãn:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, \[SA \bot (ABCD).\] Mặt phẳng qua A và vuông góc với SC cắt SB,SC,SD theo thứ tự tại H,M,K. Chọn khẳng định sai trong các khẳng định sau?
Cho hình chóp S.ABC thỏa mãn SA=SB=SC. Tam giác ABC vuông tại A. Gọi H là hình chiếu vuông góc của S lên mp(ABC). Chọn khẳng định sai trong các khẳng định sau?