Điểm thuộc đường thẳng \[d:x - y - 1 = 0\] cách đều hai điểm cực trị của đồ thị hàm số \[y = {x^3} - 3{x^2} + 2\;\] là
A.(2;1).
B. (0;−1).
C.(1;0).
D.(-1;2)
Giải bởi qa.haylamdo.com
Ta có
\[\begin{array}{l}y = {x^3} - 3{x^2} + 2 \to y\prime = 3{x^2} - 6x;y\prime = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0 \Rightarrow y(0) = 2}\\{x = 2 \Rightarrow y(2) = - 2}\end{array}} \right.\end{array}\]
Suy ra tọa độ hai điểm cực trị của đồ thị hàm số là\[A\left( {0;2} \right),\,\,B\left( {2; - \,2} \right).\]
Gọi\[M \in d \Rightarrow M\left( {a;a - 1} \right),\] khi đó\(\left\{ {\begin{array}{*{20}{c}}{MA = \sqrt {{a^2} + {{(a - 3)}^2}} }\\{MB = \sqrt {{{(a - 2)}^2} + {{(a + 1)}^2}} }\end{array}} \right.\)
Mà M cách đều A,B
Suy ra\[M{A^2} = M{B^2} \Leftrightarrow {a^2} + {\left( {a - 3} \right)^2} = {\left( {a - 2} \right)^2} + {\left( {a + 1} \right)^2} \Leftrightarrow a = 1 \Rightarrow M(1;0).\]
Đáp án cần chọn là: C
Cho hàm số \[y = f\left( x \right)\;\]có đạo hàm \[f\prime \left( x \right) = {x^2}({x^2} - 1).\] Điểm cực tiểu của hàm số \[y = f\left( x \right)\;\] là:
Đồ thị hàm số \[y = {x^3} - 2m{x^2} + {m^2}x + n\] có điểm cực tiểu là A(1;3). Giá trị của m+n bằng:
Cho hàm số bậc hai y=f(x) có đồ thị như hình vẽ bên, một hàm số g(x) xác định theo f(x) có đạo hàm \[g\prime (x) = f(x) + m\]. Tìm tất cả các giá trị thực của tham số m để hàm số g(x) không có cực trị.
Cho hàm số y=f(x) có đạo hàm \[f\prime (x) = (x - 1)({x^2} - 2)({x^4} - 4)\] Số điểm cực trị của hàm số y=f(x) là:
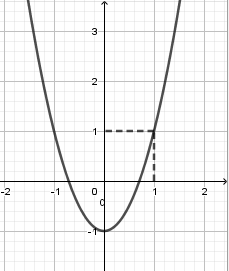
Cho các phát biểu sau:
1. Hàm số y=f(x) đạt cực đại tại \[{x_0}\] khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua \[{x_0}\].
2. Hàm số y=f(x) đạt cực trị tại \[{x_0}\] khi và chỉ khi \[{x_0}\] là nghiệm của đạo hàm.
3. Nếu \[f\prime (x0) = 0\;\] và \[f\prime \prime (x0) = 0\;\] thì \[{x_0}\] không phải là cực trị của hàm số y=f(x) đã cho.
4. Nếu f′(x0)=0 và \[f\prime \prime (xo) > 0\;\] thì hàm số đạt cực đại tại \[{x_0}\].
Các phát biểu đúng là:
Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu \[f\prime (x)\;\] như sau :
Hàm số y=f(x) có bao nhiêu điểm cực trị ?
Nếu \[{x_0}\] là điểm cực đại của hàm số thì \[({x_0};f({x_0}))\;\]là:
Điều kiện để hàm số bậc ba không có cực trị là phương trình y′=0 có:
Cho hàm số y=f(x) có đạo hàm trên (a;b). Nếu \[f\prime (x)\;\] đổi dấu từ âm sang dương qua điểm \[{x_0}\] thuộc (a;b) thì
Đồ thị hàm số \[y = {x^3} - 3x + 2\] có 2 điểm cực trị A,B. Diện tích tam giác OAB với O(0;0) là gốc tọa độ bằng:
Cho hàm số \[y = \frac{{ - {x^2} + 3x + 6}}{{x + 2}}\], chọn kết luận đúng:
Hình vẽ dưới đây mô tả số người nhiễm Covid-19 đang được điều trị ở Việt Nam tính từ ngày 23/01/2020 đến ngày 13/02/2021.
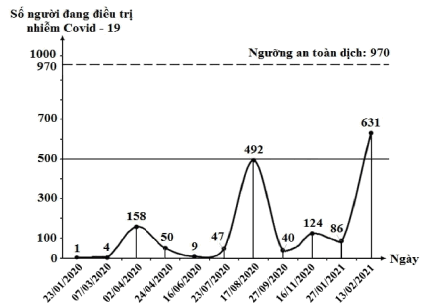
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người được điều trị Covid-19 nhiều nhất?
Cho hàm số f(x) có đạo hàm \[f\prime (x) = x(x - 1){(x + 4)^3},\forall x \in \mathbb{R}.\] Số điểm cực tiểu của hàm số đã cho là:
