Tìm a biết $I = \int\limits_{ - 1}^2 {\frac{{{e^x}dx}}{{2 + {e^x}}}} = \ln \frac{{ae + {e^3}}}{{ae + b}}$ với a,bb là các số nguyên dương.

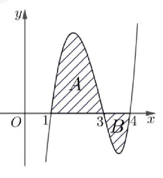
Cho hàm số y=f(x) có đồ thị như hình vẽ. Biết các miền A và B có diện tích lần lượt là 4 và 1. Tính $I = \mathop \smallint \limits_1^2 4xf\left( {{x^2}} \right)dx$

Tính tích phân $I = \mathop \smallint \limits_0^\pi {\cos ^3}x\sin xdx$

Đặt $\cos x = t \Rightarrow - \sin xdx = dt \Rightarrow \sin xdx = - dt$

Đổi cận:$\left\{ {\begin{array}{*{20}{c}}{x = 0 \Rightarrow t = 1}\\{x = \pi \Rightarrow t = - 1}\end{array}} \right.$

$\Rightarrow I = - \int\limits_1^{ - 1} {{t^3}dt = } \int\limits_{ - 1}^1 {{t^3}dt = \frac{{{t^4}}}{4}} \left| {_{ - 1}^1} \right. = \frac{1}{4} - \frac{1}{4} = 0$

Hàm số y=f(x) có nguyên hàm trên (a;b)  đồng thời thỏa mãn f(a)=f(b). Lựa chọn phương án đúng:

Cho $2\sqrt 3 m - \mathop \smallint \limits_0^1 \frac{{4{x^3}}}{{{{\left( {{x^4} + 2} \right)}^2}}}dx = 0$. Khi đó $144{m^2} - 1\;$bằng:

Cho tích phân $I = \mathop \smallint \limits_0^{\frac{\pi }{2}} \sin x\sqrt {8 + \cos x} dx$ Đặt $u = 8 + cosx$ thì kết quả nào sau đây là đúng?

Cho y=f(x) là hàm số lẻ và liên tục trên $\left[ { - a;a} \right].$Chọn kết luận đúng:

Cho tích phân $I = \mathop \smallint \limits_0^{\frac{\pi }{2}} {e^{{{\sin }^2}x}}\sin x{\cos ^3}xdx$. Nếu đổi biến số $t = si{n^2}x$ thì:

Đặt$t = {\sin ^2}x \Rightarrow dt = 2\sin x\cos xdx \Rightarrow \sin x\cos xdx = \frac{1}{2}dt$ và${\cos ^2}x = 1 - {\sin ^2}x = 1 - t$

Đổi cận: $\left\{ {\begin{array}{*{20}{c}}{x = 0 \Rightarrow t = 0}\\{x = \frac{\pi }{2} \Rightarrow t = 1}\end{array}} \right.$

Khi đó

$I = \mathop \smallint \limits_0^{\frac{\pi }{2}} {e^{{{\sin }^2}x}}\sin x{\cos ^3}xdx = \mathop \smallint \limits_0^{\frac{\pi }{2}} {e^{{{\sin }^2}x}}co{s^2}x\sin x\cos xdx = \frac{1}{2}\mathop \smallint \limits_0^1 {e^t}\left( {1 - t} \right)dt$

 $\mathop \smallint \limits_0^1 \frac{{\pi {x^3} + {2^x} + {\rm{e}}{x^3}{{.2}^x}}}{{\pi + {\rm{e}}{{.2}^x}}}{\rm{d}}x = \frac{1}{m} + \frac{1}{{{\rm{e}}\ln n}}\ln \left( {p + \frac{{\rm{e}}}{{{\rm{e}} + \pi }}} \right)$ với m, n, p là các số nguyên dương. Tính tổng $S = m + n + p$.

Cho $\mathop \smallint \nolimits_0^4 f(x)dx = - 1$, tính $I = \mathop \smallint \limits_0^1 f(4x)dx$:

Tính tích phân $I = \mathop \smallint \limits_{\ln 2}^{\ln 5} \frac{{{e^{2x}}}}{{\sqrt {{e^x} - 1} }}dx$ bằng phương pháp đổi biến số $u = \sqrt {{e^x} - 1}$. Khẳng định nào sau đây là khẳng định đúng?

Cho $I = \mathop \smallint \limits_1^e \frac{{\sqrt {1 + 3\ln x} }}{x}dx$ và $t = \sqrt {1 + 3lnx} \;$. Chọn khẳng định sai trong các khẳng định sau:

Cho hàm số f(x) liên tục trên R  và $\mathop \smallint \limits_{ - 2}^4 f(x)dx = 2$ . Mệnh đề nào sau đây là sai?

Đổi biến $u = \ln x$ thì tích phân $I = \mathop \smallint \limits_1^e \frac{{1 - \ln x}}{{{x^2}}}dx$ thành:

Cho $\mathop \smallint \limits_0^1 f\left( x \right)dx = 1.$Tính $I = \mathop \smallint \limits_0^{\frac{\pi }{4}} \left( {2{{\sin }^2}x - 1} \right)f\left( {\sin 2x} \right)dx$

Đổi biến $x = 4\sin t$ của tích phân $I = \int\limits_0^{\sqrt 8 } {\sqrt {16 - {x^2}} }$ ta được: