Kí hiệu (H)  là hình phẳng giới hạn bởi đồ thị hàm số $y = 2(x - 1){e^x}$, trục tung và trục hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình (H)  xung quanh trục Ox .

Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x=1 và x=3, biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ $x\;(1 \le x \le 3)$ thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và $\sqrt {3{x^2} - 2.}$

Cho hai hàm số $y = {f_1}\left( x \right)$và$y = {f_2}\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]\;$và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x=a,x=b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây ? 

Gọi (D₁) là hình phẳng giới hạn bởi các đường $y = 2\sqrt x ,y = 0\;{\rm{ }}v\`a \;x = 2020,$, (D₂) là hình phẳng giới hạn bởi các đường $y = \sqrt {3x} ,y = 0$ và $x = 2020.$. Gọi V₁,V₂ lần lượt là thể tích khối tròn xoay tạo thành khi quay (D₁)  và (D₂) xung quanh trục Ox. Tỉ số $\frac{{{V_1}}}{{{V_2}}}$ bằng:

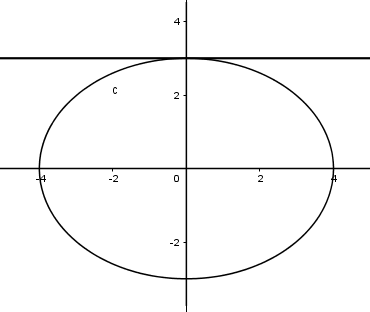
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi đường $\left( E \right):\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1$quay quanh Oy?

Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường  $y = \sqrt {2 - x} ;y = x$ xung quanh trục Ox được tính theo công thức nào sau đây?

Cho hình phẳng giới hạn bởi $D = \left\{ {y = \tan x;\,\,y = 0;\,\,x = 0;\,\,x = \frac{\pi }{3}} \right\}.$ Thể tích vật tròn xoay khi D quay quanh trục Ox là $V = \pi (a - \frac{\pi }{b}),\;$ với a,b∈R.. Tính $T = {a^2} + 2b.$.

Cho hình (H) giới hạn bởi đồ thị hàm số y=f(x) , trục hoành và hai đường thẳng x=a,x=b. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox là:

Cho hình (H) giới hạn bởi đường cong ${y^2} + x = 0$, trục Oy và hai đường thẳng y=0,y=1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Oy được tính bởi:

Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường $y = {x^2} + 1;x = 0$ và tiếp tuyến của đồ thị hàm số $y = {x^2} + 1\;$ tại điểm A(1;2) quanh trục Ox là

Cho vật thể V được giới hạn bởi hai mặt phẳng x=0 và x=−2, mặt phẳng vuông góc với trục Ox cắt V theo thiết diện $S(x) = 2{x^2}$. Thể tích của V được tính bởi:

Tính thể tích hình xuyến do quay hình tròn  có phương trình ${x^2} + {\left( {y - 2} \right)^2} = 1$ khi quanh trục Ox..

Cho hình phẳng (H) giới hạn bởi $y = \frac{1}{3}{x^3} - {x^2}\;$ và Ox.  Thể tích khối tròn xoay sinh ra khi quay (H)  quanh Ox bằng :

Cho hình (H) giới hạn bởi đồ thị hàm số $y = {x^3}$, trục hoành và hai đường thẳng x=0,x=1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox được tính bởi:

Tính thể tích khi $S = \left\{ {y = {x^2} - 4x + 6;\,\,y = - \,{x^2} - 2x + 6} \right\}$ quay quanh trục Ox.

Cho vật thể V được giới hạn bởi hai mặt phẳng x=a và x=b(a<b), mặt phẳng vuông góc với trục Ox cắt V theo thiết diện S(x). Thể tích của V được tính bởi: