Cho hàm số f(x) liên tục trên [0;3] về . Giá trị của tích phân
A. 6
B. 3
C. 4
D. 5
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com

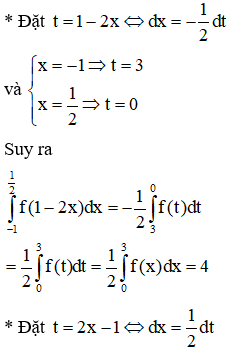

Một đa giác lồi có 10 đỉnh. Chọn ngẫu nhiên ba đỉnh của đa giác và nối chúng lại với nhau ta được một tam giác. Tính xác suất để tam giác thu được có ba cạnh là ba đường chéo của đa giác đã cho.
Trong không gian Oxyz. Cho tứ diện đều ABCD có A(0;1;2) và hình chiếu vuông góc của A trên mặt phẳng (BCD) là H (4; -3;-2). Tọa độ tâm I của mặt cầu ngoại tiếp tứ diện ABCD.
Tìm m để tiệm cận ngang của đồ thị hàm số cắt đường thẳng tại điểm có hoành độ bằng 2
Trong không gian tọa độ Oxyz, cho A(1;3;10), B(4;6;5) và M là điểm thay đổi trên mặt phẳng (Oxy) sao cho MA, MB cùng tạo với mặt phẳng (Oxy) các góc bằng nhau. Tìm giá trị nhỏ nhất của AM
Một người gửi 100 triệu đồng vào một ngân hàng với lãi suất 6%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 300 triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền ra.
Cho hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn . Biết và . Tìm tất cả các giá trị thực của tham số m để phương trình có hai nghiệm thực phân biệt.
Trong không gian Oxyz, cho điểm A(2;5;3) và đường thẳng . Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ điểm A đến (P) lớn nhất. Khoảng cách từ điểm M(1; 2; -1) đến mặt phẳng (P) bằng
Trong không gian Oxyz, biết mặt phẳng (P) đi qua điểm M(1;4;9) và cắt các tia dương Ox, Oy, Oz lần lượt tại ba điểm A, B, C khác gốc tọa độ O sao cho OA +OB+OC đạt giá trị nhỏ nhất. Khi đó chọn khẳng định đúng
Hình trụ tròn xoay có độ dài đường sinh bằng l và bán kính đáy bằng r có diện tích xung quanh Sxq cho bởi công thức
Trong không gian Oxyz, mặt phẳng Oxy cắt mặt cầu theo thiết diện là đường tròn bán kính r
Cho hàm số y = f(x) liên tục, không âm trên R thỏa mãn và f(0) = 0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [1;3] lần lượt là